Advertisements
Advertisements
Question
एक समकोण त्रिभुज में, सिद्ध कीजिए कि कर्ण के मध्य-बिंदु को उसके सम्मुख शीर्ष से मिलाने वाला रेखाखंड कर्ण का आधा होता है।
Solution
दिया गया है - ΔABC में, ∠B = 90° और D, AC का मध्य-बिंदु है।
रचना - BD को E तक इस प्रकार बढ़ाइए कि BD = DE और EC को मिला दे।
सिद्ध करना है - BD = `1/2` AC
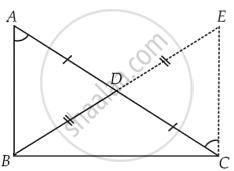
प्रमाण - ΔADB और ΔCDE में,
AD = DC ...[∵ D, AC का मध्य-बिंदु है।]
BD = DE ...[रचना द्वारा]
और ∠ADB = ∠CDE ...[शीर्षाभिमुख कोण]
∴ ΔADB ≅ ΔCDE ...[SAS सर्वांगसमता नियम द्वारा]
⇒ AB = EC ...[CPCT द्वारा]
और ∠BAD = ∠DCE ...[CPCT द्वारा]
लेकिन ∠BAD और ∠DCE एकांतर कोण हैं।
तो, EC || AB और BC एक तिर्यक रेखा है।
∴ ∠ABC + ∠BCE = 180° ...[आंतरिक कोण]
⇒ 90° + ∠BCE = 180° ...[∵ ∠ABC = 90°, दिया गया है।]
⇒ ∠BCE = 180° – 90°
⇒ ∠BCE = 90°
ΔABC और ΔECB में,
AB = EC ...[ऊपर सिद्ध किया गया]
BC = CB ...[उभयनिष्ठ पक्ष]
और ∠ABC = ∠ECB ...[प्रत्येक 90°]
∴ ΔABC ≅ ΔECB ...[SAS सर्वांगसम नियम द्वारा]
⇒ AC = EB ...[CPCT द्वारा]
⇒ `1/2` EB = `1/2` AC ...[दोनों पक्षों को 2 से विभाजित करने पर]
⇒ BD = `1/2` AC
अतः सिद्ध हुआ।
APPEARS IN
RELATED QUESTIONS
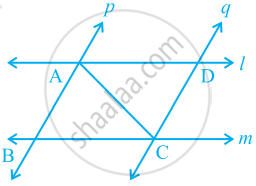
l और m दो समांतर रेखाएँ हैं जिन्हें समांतर रेखाओं p और q का एक अन्य युग्म प्रतिच्छेदित करता है (देखिए आकृति) दर्शाइए कि: △ABC ≌ △CDA है।
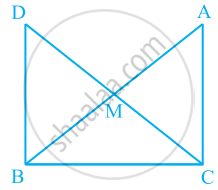
एक समकोण त्रिभुज ABC में, जिसमें कोण C समकोण है, M कर्ण AB का मध्य-बिंदु है। C को M से मिलाकर D तक इस प्रकार बढ़ाया गया है कि DM = CM है। बिंदु D को बिंदु B से मिला दिया जाता है (देखिए आकृति)। दर्शाइए कि:
- △AMC ≌ △BMD
- ∠DBC एक समकोण है।
- △DBC ≌ △ACB
- CM = `1/2` AB
ABC एक समकोण त्रिभुज है, जिसमें ∠A = 90° और AB = AC है। ∠B और ∠C ज्ञात कीजिए।
क्या भुजाओं की लंबाइयाँ 8 cm, 7 cm और 4 cm लेकर किसी त्रिभुज की रचना की जा सकती है? अपने उत्तर के लिए कारण दीजिए।
AB = AC वाले एक समद्विबाहु त्रिभुज के कोणों B और C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं। दर्शाइए कि ∠ABC के आसन्न एक बहिष्कोण ∠BOC के बराबर हैं।
निम्नलिखित आकृति में, AD कोण BAC का समद्विभाजक है। सिद्ध कीजिए कि AB > BD है।

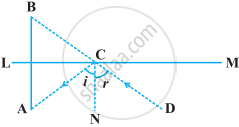
एक समतल दर्पण LM के सम्मुख स्थित बिंदु A पर रखी किसी वस्तु का प्रतिबिम्ब एक प्रेक्षक D से बिंदु B पर देखता है, जैसा कि निम्नलिखित आकृति में दर्शाया गया है। सिद्ध कीजिए कि यह प्रतिबिम्ब दर्पण के पीछे उतनी ही दूरी पर है जितनी दूरी पर वह वस्तु दर्पण के सम्मुख है।
[संकेत : CN दर्पण पर अभिलंब है। साथ ही, आपतन कोण = परावर्तन कोण।]
ABC एक समकोण त्रिभुज है, जिसमें AB = AC है। ∠A का समद्विभाजक BC से D पर मिलता है। सिद्ध कीजिए कि BC = 2AD है।
ABCD एक चतुर्भुज है, जिसमें AB = AD और CB = CD है। सिद्ध कीजिए कि AC, BD का लंब समद्विभाजक है।
