Advertisements
Advertisements
प्रश्न
AB = AC वाला ABC एक समद्विबाहु त्रिभुज है तथा D भुजा BC पर इस प्रकार स्थित है कि AD ⊥ BC है। (आकृति)। ∠BAD = ∠CAD सिद्ध करने के लिए, किसी विद्यार्थी ने निम्नलिखित प्रक्रिया अपनाई :
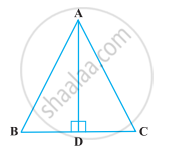
∆ABD और ∆ACD में,
AB = AC (दिया है)
∠B = ∠C (क्योंकि AB = AC)
तथा ∠ADB = ∠ADC (प्रत्येक 90°)
अतः, ∆ABD ≅ ∆ACD (AAS)
इसलिए, ∠BAD = ∠CAD (CPCT)
उपरोक्त तर्कणों में क्या कमी है?
[संकेत : याद कीजिए कि जब AB = AC हो, तो ∠B = ∠C को कैसे सिद्ध किया जाता है।]
उत्तर
∆ABC में, AB = AC है।
⇒ ∠ACB = ∠ABC ...[समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
∆ABD और ∆ACD में,
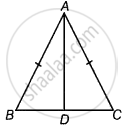
AB = AC ...[दिया गया है।]
∠ABD = ∠ACD ...[ऊपर सिद्ध]
∠ADB = ∠ADC ...[प्रत्येक 90°]
∴ ∆ABD ≅ ∆ACD ...[AAS द्वारा]
इसलिए, ∠BAD = ∠CAD ...[CPCT द्वारा]
इसलिए, दिए गए तर्क में दोष यह है कि पहले सिद्ध कीजिए कि ∠ABD = ∠ACD है।
अत:, ∠ABD = ∠ACD दोष है।
APPEARS IN
संबंधित प्रश्न
“यदि किसी त्रिभुज की दो भुजाएँ और एक कोण दूसरे त्रिभुज की दो भुजाओं और एक कोण के बराबर हों, तो दोनों त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।” क्या यह कथन सत्य है? क्यों?
क्या भुजाओं की लंबाइयाँ 4 cm, 3 cm और 7 cm लेकर किसी त्रिभुज की रचना की जा सकती है? अपने उत्तर के लिए कारण दीजिए।
यदि ∆PQR ≅ ∆EDF है, तो क्या यह कहना सत्य है कि PR = EF है? अपने उत्तर के लिए कारण दीजिए।
क्या भुजाओं की लंबाइयाँ 9 cm, 7 cm और 17 cm लेकर किसी त्रिभुज की रचना की जा सकती है? अपने उत्तर के लिए कारण दीजिए।
क्या भुजाओं की लंबाइयाँ 8 cm, 7 cm और 4 cm लेकर किसी त्रिभुज की रचना की जा सकती है? अपने उत्तर के लिए कारण दीजिए।
निम्नलिखित आकृति में, AD कोण BAC का समद्विभाजक है। सिद्ध कीजिए कि AB > BD है।

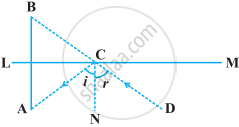
एक समतल दर्पण LM के सम्मुख स्थित बिंदु A पर रखी किसी वस्तु का प्रतिबिम्ब एक प्रेक्षक D से बिंदु B पर देखता है, जैसा कि निम्नलिखित आकृति में दर्शाया गया है। सिद्ध कीजिए कि यह प्रतिबिम्ब दर्पण के पीछे उतनी ही दूरी पर है जितनी दूरी पर वह वस्तु दर्पण के सम्मुख है।
[संकेत : CN दर्पण पर अभिलंब है। साथ ही, आपतन कोण = परावर्तन कोण।]
दो रेखाएँ l और m बिंदु O पर प्रतिच्छेद करती हैं तथा P बिंदु O से होकर जाने वाली रेखा n पर स्थित कोई बिंदु इस प्रकार है कि P रेखाओं l और m से समदूरस्थ है। सिद्ध कीजिए कि n रेखाओं l और m के बीच बनने वाले कोण का समद्विभाजक है।
ABCD एक चतुर्भुज इस प्रकार है कि विकर्ण AC दोनों कोणों A और C का समद्विभाजक है। सिद्ध कीजिए कि AB = AD और CB = CD है।
सिद्ध कीजिए कि एक समबाहु त्रिभुज को छोड़कर, किसी त्रिभुज में सबसे लंबी भुजा का सम्मुख कोण एक समकोण के `2/3` भाग से बड़ा होता हैं।
