Advertisements
Advertisements
प्रश्न
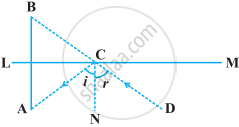
एक समतल दर्पण LM के सम्मुख स्थित बिंदु A पर रखी किसी वस्तु का प्रतिबिम्ब एक प्रेक्षक D से बिंदु B पर देखता है, जैसा कि निम्नलिखित आकृति में दर्शाया गया है। सिद्ध कीजिए कि यह प्रतिबिम्ब दर्पण के पीछे उतनी ही दूरी पर है जितनी दूरी पर वह वस्तु दर्पण के सम्मुख है।
[संकेत : CN दर्पण पर अभिलंब है। साथ ही, आपतन कोण = परावर्तन कोण।]
उत्तर १
दिया गया है - एक बिंदु OA को बिंदु A पर रखा गया है, LM एक समतल दर्पण है, D एक प्रेक्षक है और OB प्रतिबिम्ब है।
सिद्ध करना है - प्रतिबिम्ब दर्पण के पीछे उतनी ही दूरी पर बनता है जितनी कि वस्तु दर्पण के सामने होती है अर्थात् OB = OA।

प्रमाण - CN ⊥ LM और AB ⊥ LM
⇒ AB || CN
∠A = ∠i [वैकल्पिक आंतरिक कोण] ...(i)
∠B = ∠r [संगत कोण] ...(ii)
साथ ही, ∠i = ∠r [∵ आपतन कोण = परावर्तित कोण] ...(iii)
समीकरण (i), (ii) और (iii) से,
∠A = ∠B
ΔCOB और ΔCOA में,
∠B = ∠A ...[ऊपर सिद्ध]
∠1 = ∠2 ...[प्रत्येक 90°]
और CO = CO ...[सामान्य पक्ष]
∴ ΔCOB ≅ ΔCOA ...[AAS सर्वांगसमता नियम द्वारा]
⇒ OB = OA ...[CPCT द्वारा]
अतः सिद्ध हुआ।
उत्तर २
ΔOBC और ΔOAC में,
∠1 = ∠2 ...[प्रत्येक 90°]
साथ ही, ∠i = ∠r [∵ आपतन कोण = परावर्तन कोण] ...(i)
समीकरण के दोनों पक्षों (i) को –1 से गुणा करने पर और फिर दोनों पक्षों में 90° जोड़ने पर, हम प्राप्त करते हैं।
90° – ∠i = 90° – ∠r
⇒ ∠ACO = ∠BCO
और OC = OC ...[सामान्य पक्ष]
∴ ΔOBC ≅ ΔOAC ...[ASA सर्वांगसमता नियम द्वारा]
⇒ OB = OA ...[CPCT द्वारा]
अतः, प्रतिबिम्ब दर्पण के पीछे उतनी ही दूरी पर बनता है जितनी कि वस्तु दर्पण के सामने होती है।
APPEARS IN
संबंधित प्रश्न
एक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं (देखिए आकृति)। दशाईए कि CD, रेखाखंड AB को समद्विभाजित करता है।
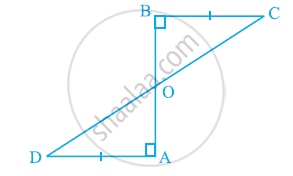
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। AP ⊥ BC खींच कर दर्शाइए कि ∠B = ∠C है।
“यदि किसी त्रिभुज की दो भुजाएँ और एक कोण दूसरे त्रिभुज की दो भुजाओं और एक कोण के बराबर हों, तो दोनों त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।” क्या यह कथन सत्य है? क्यों?
यदि ∆PQR ≅ ∆EDF है, तो क्या यह कहना सत्य है कि PR = EF है? अपने उत्तर के लिए कारण दीजिए।
∆PQR में, ∠P = 70° और ∠R = 30° है। इस त्रिभुज की कौन-सी भुजा सबसे लंबी है? अपने उत्तर के लिए कारण दीजिए।
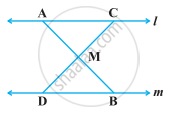
निम्नलिखित आकृति में, l || m है तथा M रेखाखंड AB का मध्य-बिंदु है। दर्शाइए कि M किसी भी रेखाखंड CD का मध्य-बिंदु है जिसके अंत:बिंदु क्रमश : l और m पर स्थित है।
AB = AC वाले एक समद्विबाहु त्रिभुज के कोणों B और C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं। दर्शाइए कि ∠ABC के आसन्न एक बहिष्कोण ∠BOC के बराबर हैं।
ABC एक समकोण त्रिभुज है, जिसमें AB = AC है। ∠A का समद्विभाजक BC से D पर मिलता है। सिद्ध कीजिए कि BC = 2AD है।
एक समकोण त्रिभुज में, सिद्ध कीजिए कि कर्ण के मध्य-बिंदु को उसके सम्मुख शीर्ष से मिलाने वाला रेखाखंड कर्ण का आधा होता है।
