Advertisements
Advertisements
प्रश्न
AB = AC वाले एक समद्विबाहु त्रिभुज के कोणों B और C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं। दर्शाइए कि ∠ABC के आसन्न एक बहिष्कोण ∠BOC के बराबर हैं।
उत्तर
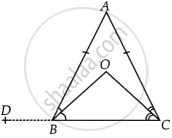
दिया गया है - ΔABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC, BO और CO क्रमश: ∠ABC और ∠ACB के समद्विभाजक हैं जो O पर प्रतिच्छेद करते हैं।
दिखाएँ के लिए - ∠DBA = ∠BOC
उत्पादन - रेखा CB का उत्पादन D पर किया गया था।
उपपत्ति - ΔABC में, AB = AC ...[दिया गया है।]
∠ACB = ∠ABC ...[समान भुजाओं के सम्मुख कोण बराबर होते हैं।]
⇒ `1/2 ∠ACB = 1/2 ∠ABC` ...[दोनों पक्षों को 2 से भाग देने पर]
⇒ ∠OCB = ∠OBC ...(i) [∵ BO और CO, ∠ABC और ∠ACB के समद्विभाजक हैं।]
∆BOC में, ∠OBC + ∠OCB + ∠BOC = 180° ...[त्रिभुज के कोण योग गुण द्वारा]
⇒ ∠OBC + ∠OBC + ∠BOC = 180° ...[समीकरण (i) से]
⇒ 2∠OBC + ∠BOC = 180°
⇒ ∠ABC + ∠BOC = 180° ...[∵ BO, ∠ABC का समद्विभाजक है।]
⇒ 180° – ∠DBA + ∠BOC = 180° ...[∵ DBC एक सरल रेखा है।]
⇒ – ∠DBA + ∠BOC = 0
⇒ ∠DBA = ∠BOC
APPEARS IN
संबंधित प्रश्न
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। AP ⊥ BC खींच कर दर्शाइए कि ∠B = ∠C है।
क्या भुजाओं की लंबाइयाँ 9 cm, 7 cm और 17 cm लेकर किसी त्रिभुज की रचना की जा सकती है? अपने उत्तर के लिए कारण दीजिए।
∆PQR की भुजा QR पर S कोई बिंदु स्थित है। दर्शाइए कि PQ + QR + RP > 2PS है।
AB = AC वाले एक ∆ABC की भुजा, AC पर D कोई बिंदु स्थित है। दर्शाइए कि CD < BD है।
AB = AC वाले एक समद्विबाहु त्रिभुज के कोणों B और C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं। BO को एक बिंदु M तक बढ़ाया जाता है। सिद्ध कीजिए कि ∠MOC = ∠ABC है।
सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा की संगत माध्यिका के दोगुने से बड़ा होता हैं।
दर्शाइए कि एक चतुर्भुज ABCD में, AB + BC + CD + DA > AC + BD होता है।
ABCD एक चतुर्भुज इस प्रकार है कि विकर्ण AC दोनों कोणों A और C का समद्विभाजक है। सिद्ध कीजिए कि AB = AD और CB = CD है।
AB और CD क्रमश : एक चतुर्भुज ABCD की सबसे छोटी और सबसे बड़ी भुजाएं हैं। ∠B और ∠D में से निश्चित कीजिए कि कौन बड़ा हैं।
सिद्ध कीजिए कि एक समबाहु त्रिभुज को छोड़कर, किसी त्रिभुज में सबसे लंबी भुजा का सम्मुख कोण एक समकोण के `2/3` भाग से बड़ा होता हैं।
