Advertisements
Advertisements
प्रश्न
P कोण ABC के समद्विभाजक पर स्थित कोई बिंदु है। यदि P से होकर BA के समांतर खींची गई रेखा BC से Q पर मिलती है, तो सिद्ध कीजिए कि BPQ एक समद्विबाहु त्रिभुज है।
बेरीज
उत्तर
प्रश्न में दिया गया है, P, ∠ABC के समद्विभाजक पर स्थित एक बिंदु है। यदि P से होकर BA के समान्तर रेखा BC को Q पर मिलती है।
सिद्ध करना है - BPQ एक समद्विबाहु त्रिभुज है।
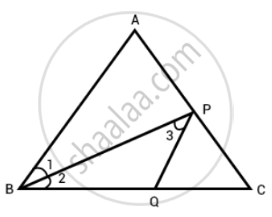
उपपत्ति - ∠1 = ∠2 ...(i) [BP, ∠ABC का समद्विभाजक है।]
PQ, BA के समानांतर है और BP उन्हें काटता है।
इसलिए, ∠1 = ∠3 ...[वैकल्पिक आंतरिक कोण के रूप में PQ || AB]
∠2 = ∠3 ...[ऊपर सिद्ध]
PQ = BQ ...[समान कोण की सम्मुख भुजाएँ बराबर होती हैं।]
अत:, BPQ एक समद्विबाहु त्रिभुज है।
shaalaa.com
त्रिभुजों की सर्वांगसमता के लिए प्रतिबंध
या प्रश्नात किंवा उत्तरात काही त्रुटी आहे का?