Advertisements
Advertisements
प्रश्न
आकृति में, AC = AE, AB = AD और ∠BAD = ∠EAC है। दर्शाइए कि BC = DE है।
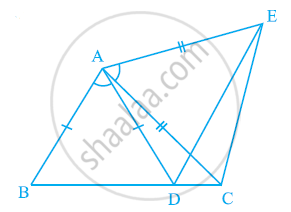
उत्तर
दिया है कि
∠BAD = ∠EAC
दोनों पक्षों में, ∠DAC जोडने पर हमें प्राप्त होता है।
∠BAD + ∠DAC = ∠EAC + ∠DAC
⇒ ∠BAC = ∠EAD …(I)
अब, △ABC और △AED में,
AB = AD ...[दिया है।]
AC = AE ...[दिया है।]
∠BAC = ∠EAD ...[(I) से]
∴ △ABC ≌ △ADE ...[AAS सर्वांगसम नियम से]
⇒ BC = DE ...[सर्वांगसम त्रिभुजों के संगत भाग]
APPEARS IN
संबंधित प्रश्न
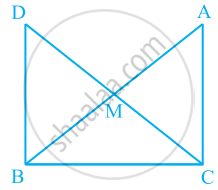
एक समकोण त्रिभुज ABC में, जिसमें कोण C समकोण है, M कर्ण AB का मध्य-बिंदु है। C को M से मिलाकर D तक इस प्रकार बढ़ाया गया है कि DM = CM है। बिंदु D को बिंदु B से मिला दिया जाता है (देखिए आकृति)। दर्शाइए कि:
- △AMC ≌ △BMD
- ∠DBC एक समकोण है।
- △DBC ≌ △ACB
- CM = `1/2` AB
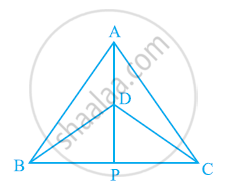
△ABC और △DBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं (देखिए आकृति)। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि:
- △ABD ≌ △ACD
- △ABP ≌ △ACP
- AP कोण A और कोण D दोनों को समद्विभाजित करता है।
- AP रेखाखंड BC का लम्ब समद्विभाजक है।
“यदि किसी त्रिभुज की दो भुजाएँ और एक कोण दूसरे त्रिभुज की दो भुजाओं और एक कोण के बराबर हों, तो दोनों त्रिभुज अवश्य ही सर्वांगसम होने चाहिए।” क्या यह कथन सत्य है? क्यों?
∆ABC ≅ ∆RPQ दिया हुआ है। क्या यह कहना सत्य है कि BC = QR है? क्यों?
AD किसी त्रिभुज ABC की एक माध्यिका है। क्या यह कहना सत्य है कि AB + BC + CA > 2AD है? अपने उत्तर के लिए कारण दीजिए।
क्या भुजाओं की लंबाइयाँ 8 cm, 7 cm और 4 cm लेकर किसी त्रिभुज की रचना की जा सकती है? अपने उत्तर के लिए कारण दीजिए।
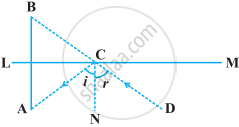
एक समतल दर्पण LM के सम्मुख स्थित बिंदु A पर रखी किसी वस्तु का प्रतिबिम्ब एक प्रेक्षक D से बिंदु B पर देखता है, जैसा कि निम्नलिखित आकृति में दर्शाया गया है। सिद्ध कीजिए कि यह प्रतिबिम्ब दर्पण के पीछे उतनी ही दूरी पर है जितनी दूरी पर वह वस्तु दर्पण के सम्मुख है।
[संकेत : CN दर्पण पर अभिलंब है। साथ ही, आपतन कोण = परावर्तन कोण।]
O एक वर्ग ABCD के अभ्यंतर में स्थित बिंदु इस प्रकार है कि OAB एक समबाहु त्रिभुज है। सिद्ध कीजिए कि ∆OCD एक समद्विबाहु त्रिभुज है।
ABC और DBC एक ही आधार BC पर स्थित दो त्रिभुज इस प्रकार हैं कि बिंदु A और D आधार BC के विपरीत ओर स्थित हैं, AB = AC और DB = DC है। दर्शाइए कि AD रेखाखंड BC का लंब समद्विभाजक है।
दर्शाइए कि एक चतुर्भुज ABCD में, AB + BC + CD + DA > AC + BD होता है।
