Advertisements
Advertisements
प्रश्न
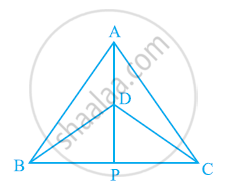
△ABC और △DBC एक ही आधार BC पर बने दो समद्विबाहु त्रिभुज इस प्रकार हैं कि A और D भुजा BC के एक ही ओर स्थित हैं (देखिए आकृति)। यदि AD बढ़ाने पर BC को P पर प्रतिच्छेद करे, तो दर्शाइए कि:
- △ABD ≌ △ACD
- △ABP ≌ △ACP
- AP कोण A और कोण D दोनों को समद्विभाजित करता है।
- AP रेखाखंड BC का लम्ब समद्विभाजक है।
उत्तर
(i) ΔABD और ΔACD में,
AB = AC ...(दिया गया है)
BD = CD ...(दिया गया है)
AD = AD ..(उभयनिष्ठ)
∴ ΔABD ≅ ΔACD ...(SSS सर्वांगसमता नियम द्वारा)
⇒ ∠BAD = ∠CAD ...(सर्वांगसम त्रिभुजों के संगत भागों द्वारा)
⇒ ∠BAP = ∠CAP …(1)
(ii) ΔABP और ΔACP में,
AB = AC ...(दिया गया है)
∠BAP = ∠CAP ...[समीकरण (1) से]
AP = AP ...(उभयनिष्ठ)
∴ ΔABP ≅ ΔACP ...(SSS सर्वांगसमता नियम द्वारा)
⇒ BP = CP ...(सर्वांगसम त्रिभुजों के संगत भागों द्वारा) …(2)
(iii) समीकरण (1) से,
∠BAP = ∠CAP
अतः AP, ∠A को समद्विभाजित करता है।
ΔBDP और ΔCDP में,
BD = CD ...(दिया गया है)
DP = DP ...(उभयनिष्ठ)
BP = CP ...[समीकरण (2) से]
∴ ΔBDP ≅ ΔCDP ...(SSS सर्वांगसमता नियम द्वारा)
⇒ ∠BDP = ∠CDP ...(सर्वांगसम त्रिभुजों के संगत भागों द्वारा) …(3)
अतः AP, ∠D को समद्विभाजित करता है।
(iv) ΔBDP ≅ ΔCDP
∴ ∠BPD = ∠CPD ...(सर्वांगसम त्रिभुजों के संगत भागों द्वारा) …(4)
∠BPD + ∠CPD = 180° ...(रैखिक युग्म कोण)
∠BPD + ∠BPD = 180°
2∠BPD = 180° ...[समीकरण (4) से]
∠BPD = 90° …(5)
समीकरण (2) और (5) से यह कहा जा सकता है कि AP, BC का लम्ब समद्विभाजक है।
APPEARS IN
संबंधित प्रश्न
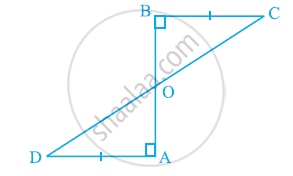
एक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं (देखिए आकृति)। दशाईए कि CD, रेखाखंड AB को समद्विभाजित करता है।
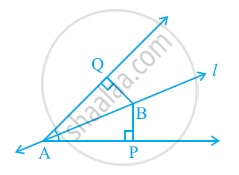
रेखा l कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिंदु है। BP और BQ कोण A की भुजाओं पर B से डाले गए लंब हैं। (देखिए आकृति) दर्शाइए कि:
- △APB ≌ △AQB
- BP = BQ है, अर्थात् बिंदु B कोण की भुजाओं से समदूरस्थ है।
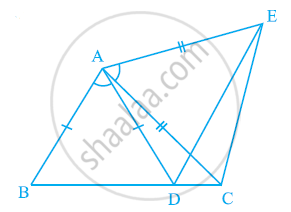
आकृति में, AC = AE, AB = AD और ∠BAD = ∠EAC है। दर्शाइए कि BC = DE है।
∆PQR में, ∠P = 70° और ∠R = 30° है। इस त्रिभुज की कौन-सी भुजा सबसे लंबी है? अपने उत्तर के लिए कारण दीजिए।
M किसी त्रिभुज ABC की भुजा BC पर स्थित एक बिंदु ऐसा है कि AM कोण BAC का समद्विभाजक है। क्या यह कहना सत्य है कि त्रिभुज का परिमाप 2 AM से अधिक है? अपने उत्तर के लिए कारण दीजिए।
AB = AC वाले एक ∆ABC की भुजा, AC पर D कोई बिंदु स्थित है। दर्शाइए कि CD < BD है।
AB = AC वाले एक समद्विबाहु त्रिभुज के कोणों B और C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं। दर्शाइए कि ∠ABC के आसन्न एक बहिष्कोण ∠BOC के बराबर हैं।
ABC और DBC एक ही आधार BC पर स्थित दो त्रिभुज इस प्रकार हैं कि बिंदु A और D आधार BC के विपरीत ओर स्थित हैं, AB = AC और DB = DC है। दर्शाइए कि AD रेखाखंड BC का लंब समद्विभाजक है।
ABCD एक चतुर्भुज है, जिसमें AB = AD और CB = CD है। सिद्ध कीजिए कि AC, BD का लंब समद्विभाजक है।
