Advertisements
Advertisements
प्रश्न
दर्शाइए कि एक चतुर्भुज ABCD में, AB + BC + CD + DA < 2(BD + AC) होता है।
उत्तर
दिया गया है - ABCD एक चतुर्भुज है।
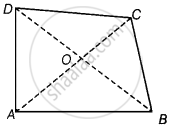
दिखाने के लिए - AB + BC + CD + DA < 2(BD + AC)
रचना - विकर्ण AC और BD को मिलाइए।
उपपत्ति - ΔOAB में, OA + OB > AB ...(i) [त्रिभुज की दो भुजाओं का योग तीसरी भुजा से बड़ा होता है।
∆OBC में, OB + OC > BC ...(ii) [त्रिभुज की दो भुजाओं का योग तीसरी भुजा से बड़ा होता है।]
ΔOCD में, OC + OD > CD ...(iii) [त्रिभुज की दो भुजाओं का योग तीसरी भुजा से बड़ा होता है।]
ΔODA में, OD + OA > DA ...(iv) [त्रिभुज की दो भुजाओं का योग तीसरी भुजा से बड़ा होता है।]
समीकरणों (i), (ii), (iii) और (iv) को जोड़ने पर, हम पाते हैं।
2[(OA + OB + OC + OD] > AB + BC + CD + DA
⇒ 2[(OA + OC) + (OB + OD)] > AB + BC + CD + DA
⇒ 2(AC + BD) > AB + BC + CD + DA ...[∵ OA + OC = AC और OB + OD = BD]
⇒ AB + BC + CD + DA < 2(BD + AC)
APPEARS IN
संबंधित प्रश्न
∆PQR में, ∠P = 70° और ∠R = 30° है। इस त्रिभुज की कौन-सी भुजा सबसे लंबी है? अपने उत्तर के लिए कारण दीजिए।
M किसी त्रिभुज ABC की भुजा BC पर स्थित एक बिंदु ऐसा है कि AM कोण BAC का समद्विभाजक है। क्या यह कहना सत्य है कि त्रिभुज का परिमाप 2 AM से अधिक है? अपने उत्तर के लिए कारण दीजिए।
AB = AC वाले एक समद्विबाहु त्रिभुज के कोणों B और C के समद्विभाजक परस्पर O पर प्रतिच्छेद करते हैं। दर्शाइए कि ∠ABC के आसन्न एक बहिष्कोण ∠BOC के बराबर हैं।
एक समबाहु त्रिभुज के सभी कोण ज्ञात कीजिए।
ABCD एक चतुर्भुज है, जिसमें AB = BC और AD = CD है। दर्शाइए कि BD दोनों कोणों ABC और ADC को समद्विभाजित करता है।
ABC एक समद्विबाहु त्रिभुज है, जिसमें AC = BC है। AD और BE क्रमश : BC और AC पर शीर्षलंब हैं। सिद्ध कीजिए कि AE = BD है।
सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा की संगत माध्यिका के दोगुने से बड़ा होता हैं।
एक त्रिभुज ABC में, D भुजा AC का मध्य-बिंदु है ताकि BD = `1/2` AC है। दर्शाइए कि ∠ABC एक समकोण है।
एक समकोण त्रिभुज में, सिद्ध कीजिए कि कर्ण के मध्य-बिंदु को उसके सम्मुख शीर्ष से मिलाने वाला रेखाखंड कर्ण का आधा होता है।
दो रेखाएँ l और m बिंदु O पर प्रतिच्छेद करती हैं तथा P बिंदु O से होकर जाने वाली रेखा n पर स्थित कोई बिंदु इस प्रकार है कि P रेखाओं l और m से समदूरस्थ है। सिद्ध कीजिए कि n रेखाओं l और m के बीच बनने वाले कोण का समद्विभाजक है।
