Advertisements
Advertisements
प्रश्न
सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा की संगत माध्यिका के दोगुने से बड़ा होता हैं।
उत्तर
दिया गया है - त्रिभुज ABC में माध्यिका AD के साथ,
उपपत्ति के लिए - AB + AC > 2AD
AB + BC > 2AD
BC + AC > 2AD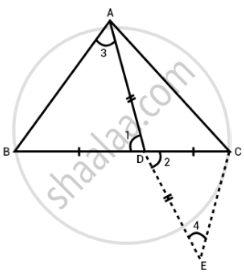
AD को E में इस प्रकार बढ़ाइए कि DE = AD और EC को मिलाइए।
उपपत्ति - त्रिभुज ADB और त्रिभुज EDC में,
AD = ED ...[रचना द्वारा]
∠1 = ∠2 ...[शीर्षाभिमुख कोण बराबर होते हैं।]
DB = DC ...[दिया गया है।]
इसलिए, सर्वांगसमता की SAS कसौटी से,
ΔADB ≅ ΔEDC
AB = EC ...[CPCT]
और ∠3 = ∠4 ...[CPCT]
पुनः, त्रिभुज AEC में,
AC + CE > AE ...[त्रिभुज की किन्हीं दो भुजाओं की लंबाई का योग तीसरी भुजा से अधिक होना चाहिए]
AC + CE > AD + DE
AC + CE > AD + AD ...[AD = DE]
AC + CE > 2AD
AC + AB > 2AD ...[क्योंकि AB = CE]
अतः सिद्ध हुआ।
इसी प्रकार, AB + BC > 2AD और BC + AC > 2AD।
APPEARS IN
संबंधित प्रश्न
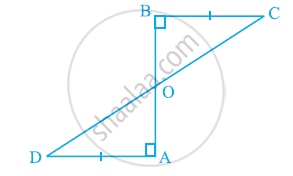
एक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं (देखिए आकृति)। दशाईए कि CD, रेखाखंड AB को समद्विभाजित करता है।
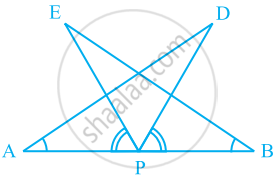
AB एक रेखाखंड है और P इसका मध्य-बिंदु है। D और E रेखाखंड AB के एक ही ओर स्थित दो बिंदु इस प्रकार हैं कि ∠BAD = ∠ABE और ∠EPA = ∠DPB है। (देखिए आकृति)। दर्शाइए कि:
- △DAP ≌ △EBP
- AD = BE
क्या भुजाओं की लंबाइयाँ 9 cm, 7 cm और 17 cm लेकर किसी त्रिभुज की रचना की जा सकती है? अपने उत्तर के लिए कारण दीजिए।
∆PQR की भुजा QR पर S कोई बिंदु स्थित है। दर्शाइए कि PQ + QR + RP > 2PS है।
एक समबाहु त्रिभुज के सभी कोण ज्ञात कीजिए।
O एक वर्ग ABCD के अभ्यंतर में स्थित बिंदु इस प्रकार है कि OAB एक समबाहु त्रिभुज है। सिद्ध कीजिए कि ∆OCD एक समद्विबाहु त्रिभुज है।
ABC और DBC एक ही आधार BC पर स्थित दो त्रिभुज इस प्रकार हैं कि बिंदु A और D आधार BC के विपरीत ओर स्थित हैं, AB = AC और DB = DC है। दर्शाइए कि AD रेखाखंड BC का लंब समद्विभाजक है।
ABC एक समद्विबाहु त्रिभुज है, जिसमें AC = BC है। AD और BE क्रमश : BC और AC पर शीर्षलंब हैं। सिद्ध कीजिए कि AE = BD है।
दो रेखाएँ l और m बिंदु O पर प्रतिच्छेद करती हैं तथा P बिंदु O से होकर जाने वाली रेखा n पर स्थित कोई बिंदु इस प्रकार है कि P रेखाओं l और m से समदूरस्थ है। सिद्ध कीजिए कि n रेखाओं l और m के बीच बनने वाले कोण का समद्विभाजक है।
