Advertisements
Advertisements
प्रश्न
AB और CD क्रमश : एक चतुर्भुज ABCD की सबसे छोटी और सबसे बड़ी भुजाएं हैं। ∠B और ∠D में से निश्चित कीजिए कि कौन बड़ा हैं।
उत्तर
दिया गया है - चतुर्भुज ABCD में, AB सबसे छोटी भुजा है और CD सबसे बड़ी भुजा है।
ज्ञात करना है - ∠B > ∠D या ∠D > ∠B।
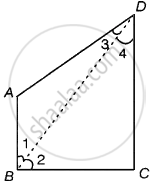
रचना - BD को मिलाइए।
अब, ΔABD में, AD > AB ...[चूँकि AB, ABCD में सबसे छोटी भुजा है।]
⇒ ∠1 > ∠3 [बड़ी भुजा का सम्मुख कोण बड़ा होता है] ...(i)
ΔBCD में, CD > BC ...[चूँकि, ABCD में CD सबसे बड़ी भुजा है।]
⇒ ∠2 > ∠4 [बड़ी भुजा का सम्मुख कोण बड़ा होता है।] ...(ii)
समीकरण (i) और (ii) को जोड़ने पर, हम प्राप्त करते हैं।
∠1 + ∠2 > ∠3 + ∠4
अत:, ∠B > ∠D
APPEARS IN
संबंधित प्रश्न
एक रेखाखंड AB पर AD और BC दो बराबर लंब रेखाखंड हैं (देखिए आकृति)। दशाईए कि CD, रेखाखंड AB को समद्विभाजित करता है।
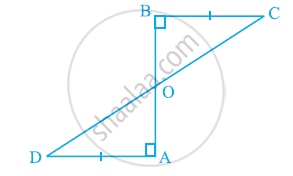
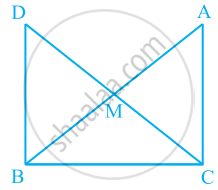
एक समकोण त्रिभुज ABC में, जिसमें कोण C समकोण है, M कर्ण AB का मध्य-बिंदु है। C को M से मिलाकर D तक इस प्रकार बढ़ाया गया है कि DM = CM है। बिंदु D को बिंदु B से मिला दिया जाता है (देखिए आकृति)। दर्शाइए कि:
- △AMC ≌ △BMD
- ∠DBC एक समकोण है।
- △DBC ≌ △ACB
- CM = `1/2` AB
ABC एक समकोण त्रिभुज है, जिसमें ∠A = 90° और AB = AC है। ∠B और ∠C ज्ञात कीजिए।
ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC है। AP ⊥ BC खींच कर दर्शाइए कि ∠B = ∠C है।
त्रिभुजों ABC और PQR में, ∠A = ∠Q और ∠B = ∠R है। ∆PQR की कौन सी भुजा ∆ABC की भुजा AB के बराबर होनी चाहिए कि दोनों त्रिभुज सर्वांगसम हों? अपने उत्तर के लिए कारण दीजिए।
AD किसी त्रिभुज ABC की एक माध्यिका है। क्या यह कहना सत्य है कि AB + BC + CA > 2AD है? अपने उत्तर के लिए कारण दीजिए।
ABC और DBC एक ही आधार BC पर स्थित दो त्रिभुज इस प्रकार हैं कि बिंदु A और D आधार BC के विपरीत ओर स्थित हैं, AB = AC और DB = DC है। दर्शाइए कि AD रेखाखंड BC का लंब समद्विभाजक है।
सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं का योग तीसरी भुजा की संगत माध्यिका के दोगुने से बड़ा होता हैं।
ABC एक समकोण त्रिभुज है, जिसमें AB = AC है तथा ∠C का समद्विभाजक भुजा AB को D पर प्रतिच्छेद करता है। सिद्ध कीजिए कि AC + AD = BC है।
ABCD एक चतुर्भुज है, जिसमें AB = AD और CB = CD है। सिद्ध कीजिए कि AC, BD का लंब समद्विभाजक है।
