Advertisements
Advertisements
प्रश्न
ABC एक समकोण त्रिभुज है, जिसमें ∠A = 90° और AB = AC है। ∠B और ∠C ज्ञात कीजिए।
उत्तर
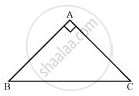
ABC एक समकोण त्रिभुज है, जिसमें
∠A = 90°
और AB = AC
△ABC में,
AB = AC
⇒ ∠C = ∠B …(I) ...[समान भुजाओं के सम्मुख कोण]
अब, △ABC में,
∠A + ∠B + ∠C = 180° ...[कोण योगफल गुण]
⇒ 90° + ∠B + ∠B = 180° ...[∵ ∠A = 90° (दिया है) और ∠B = ∠C (I) से]
⇒ 2∠B = 180° – 90°
⇒ 2∠B = 90°
⇒ ∠B = 45°
साथ ही, ∠C = ∠B
⇒ ∠C = 45°
APPEARS IN
संबंधित प्रश्न
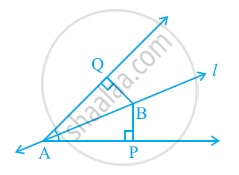
रेखा l कोण A को समद्विभाजित करती है और B रेखा l पर स्थित कोई बिंदु है। BP और BQ कोण A की भुजाओं पर B से डाले गए लंब हैं। (देखिए आकृति) दर्शाइए कि:
- △APB ≌ △AQB
- BP = BQ है, अर्थात् बिंदु B कोण की भुजाओं से समदूरस्थ है।
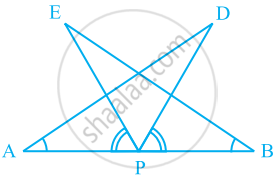
AB एक रेखाखंड है और P इसका मध्य-बिंदु है। D और E रेखाखंड AB के एक ही ओर स्थित दो बिंदु इस प्रकार हैं कि ∠BAD = ∠ABE और ∠EPA = ∠DPB है। (देखिए आकृति)। दर्शाइए कि:
- △DAP ≌ △EBP
- AD = BE
AD एक समद्विबाहु त्रिभुज ABC का एक शीर्षलम्ब है, जिसमें AB = AC है। दर्शाइए कि:
- AD रेखाखंड BC को समद्विभाजित करता है।
- AD कोण A को समद्विभाजित करता है।
- ∆ABM ≅ ∆PQN
- ∆ABC ≅ ∆PQR
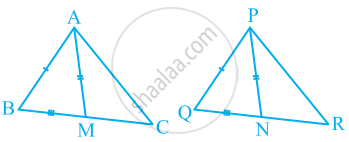
त्रिभुजों ABC और PQR में, ∠A = ∠Q और ∠B = ∠R है। ∆PQR की कौन सी भुजा ∆ABC की भुजा AB के बराबर होनी चाहिए कि दोनों त्रिभुज सर्वांगसम हों? अपने उत्तर के लिए कारण दीजिए।
AD किसी त्रिभुज ABC की एक माध्यिका है। क्या यह कहना सत्य है कि AB + BC + CA > 2AD है? अपने उत्तर के लिए कारण दीजिए।
निम्नलिखित आकृति में, AD कोण BAC का समद्विभाजक है। सिद्ध कीजिए कि AB > BD है।

O एक वर्ग ABCD के अभ्यंतर में स्थित बिंदु इस प्रकार है कि OAB एक समबाहु त्रिभुज है। सिद्ध कीजिए कि ∆OCD एक समद्विबाहु त्रिभुज है।
ABC और DBC एक ही आधार BC पर स्थित दो त्रिभुज इस प्रकार हैं कि बिंदु A और D आधार BC के विपरीत ओर स्थित हैं, AB = AC और DB = DC है। दर्शाइए कि AD रेखाखंड BC का लंब समद्विभाजक है।
एक समलंब ABCD की क्रमशः समांतर भुजाओं AB और DC के मध्य-बिंदुओं M और N को मिलाने वाला रेखाखंड दोनों भुजाओं AB और DC पर लंब है। सिद्ध कीजिए कि AD = BC है।
