Advertisements
Advertisements
प्रश्न
ΔABC मध्ये ∠A = 90°. `square`DEFG या चौरसाचे D व E हे शिरोबिंदू बाजू BC वर आहेत. बिंदू F हा बाजू AC वर आणि बिंदू G हा बाजू AB वर आहे. तर सिद्ध करा. DE2 = BD × EC (ΔGBD व ΔCFE हे समरूप दाखवा. GD = FE = DE याचा उपयोग करा.)
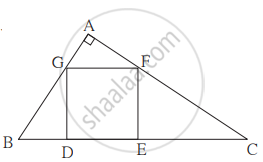
उत्तर
`square`DEFG हा चौरस आहे.
∴ DE = EF = GF = GD .....(i) [चौरसाच्या बाजू]
∠GDE = ∠DEF = 90° ..........[चौरसाचे कोन]
∴ रेख GD ⊥ रेख BC, रेख FE ⊥ रेख BC ....(ii)
ΔBAC व ΔBDG मध्ये,
∠BAC ≅ ∠BDG ....[(ii) वरून, प्रत्येक कोन 90° चा असेल.]
∠ABC ≅ ∠DBG ...[सामाईक कोन]
∴ ΔBAC ∼ ΔBDG ....(iii) [समरूपतेची कोको कसोटी]
ΔBAC व ΔFEC मध्ये,
∠BAC ≅ ∠FEC ...[(ii) वरून, प्रत्येक कोन 90° चा असेल.]
∠ACB ≅ ∠ECF ....[सामाईक कोन]
∴ ΔBAC ∼ ΔFEC ....(iv) [समरूपतेची कोको कसोटी]
∴ ΔBDG ∼ ΔFEC ....[(iii) व (iv) वरून]
∴ `"BD"/"EF" = "GD"/"EC"` ....(v) [समरूप त्रिकोणांच्या संगत बाजू]
∴ `"BD"/"DE" = "DE"/"EC"` .....[(i) व (v) वरून]
∴ DE2 = BD × EC
APPEARS IN
संबंधित प्रश्न
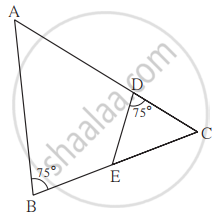
आकृती मध्ये ∠ABC = 75°, ∠EDC =75° तर कोणते दोन त्रिकोण कोणत्या कसोटीनुसार समरूप आहेत? त्यांची समरूपता योग्य एकास एक संगतीत लिहा.
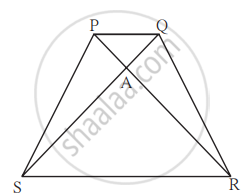
आकृतीत समलंब चौकोन PQRS मध्ये, बाजू PQ || बाजू SR, AR = 5AP, AS = 5AQ तर सिद्ध करा, SR = 5PQ.
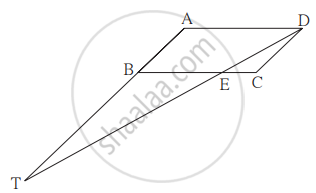
`square"ABCD"` हा समांतरभुज चौकोन आहे. बाजू BC वर E हा एक बिंदू आहे, रेषा DE ही किरण AB ला T बिंदूत छेदते. तर DE × BE = CE × TE दाखवा.
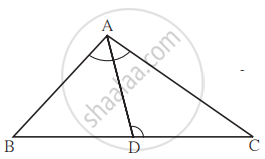
आकृतीत Δ ABC मध्ये बाजू BC वर D हा बिंदू असा आहे, की ∠BAC = ∠ADC तर सिद्ध करा, CA2 = CB × CD.
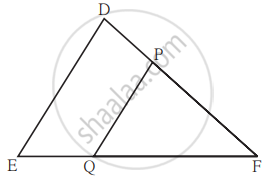
आकृती मध्ये रेख PQ || रेख DE, A (Δ PQF) = 20 एकक, जर PF = 2 DP आहे, तर A(`square"DPQE"`) काढण्यासाठी खालील कृती पूर्ण करा.
A(Δ PQF) = 20 एकक, PF = 2 DP, DP = x मानू. ∴ PF = 2x
DF = DP + `square` = `square` + `square` = 3x
Δ FDE व Δ FPQ मध्ये
∠ FDE ≅ ∠`square` (संगत कोन)
∠ FED ≅ ∠`square` (संगत कोन)
∴ Δ FDE ∼ Δ FPQ .............(कोको कसोटी)
∴ `("A"(Δ"FDE"))/("A"(Δ"FPQ")) = square/square = ((3"x")^2)/((2"x")^2) = 9/4`
A(Δ FDE) = `9/4` × A(Δ FPQ ) = `9/4 xx square = square`
A(`square` DPQE) = A(Δ FDE) - A(Δ FPQ)
= `square - square`
= `square`
आकृती मध्ये रेख XY || रेख BC तर खालील पैकी कोणते विधान सत्य आहे?
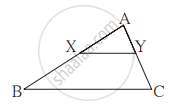
आकृती मध्ये XY || बाजू AC. जर 2AX = 3BX आणि XY = 9 तर AC ची किंमत काढण्यासाठी खालील कृती पूर्ण करा.

कृती : 2AX = 3BX
∴ `"AX"/"BX" = square/square`
`("AX" + "BX")/"BX" = (square + square)/square` ......(योग क्रिया करून)
`"AB"/"BX" = square/square` ......(I)
ΔBCA ~ ΔBYX .......(समरूपतेची `square` कसोटी)
∴ `"BA"/"BX" = "AC"/"XY"` ..........(समरूप त्रिकोणाच्या संगत बाजू)
∴ `square/square = "AC"/9`
∴ AC = `square` ..........(I) वरून
जर ΔABC ∼ ΔDEF आणि ∠A = 48°, तर ∠D = ______.

वरील आकृतीत, ΔABC मध्ये रेख XY || बाजू AC, जर 2AX = 3BX आणि XY = 9, तर AC ची किंमत काढा.

