Advertisements
Advertisements
प्रश्न
An electron in an atom is revolving around the nucleus in a circular orbit of a radius of 5.3 x 10-11 m, with a speed of 2 x 106 m/s. Find the resultant orbital magnetic moment and angular momentum of the electron. [e = 1.6 x 10-19 C, me= 9.1 x 10-31 kg]
उत्तर १
- Data: r = 5.3 × 10-11 m, v = 2 × 106 m/s,
e = 1.6 × 10-19 C, me = 9.1 × 10-31 kg
The orbital magnetic moment of the electron is
`"M"_0 = 1/2`evr
`= 1/2(1.6 xx 10^-19)(2xx10^6)(5.3 xx 10^-11)`
= 8.48 × 10-24 A.m2
The angular momentum of the electron is
L0 = mevr
= (9.1 × 10-31)(2 × 106)(5.3 × 10-11)
= 96.46 × 10-36 = 9.646 × 10-35 kg.m2/s
उत्तर २
Given:
r = `5.3 xx 10^-11` m,
v = `2 xx 10^6` ms-1,
e = `1.6 xx 10^-19` C,
me = `9.1 xx 10^-31` kg
To find:
- Orbital magnetic moment (morb)
- Angular momentum of electron
Formulae:
- morb = `"evr"/2`
- L = mvr
Calculation:
From formula (i),
morb = `(1.6 xx 10^-19 xx 2 xx 10^6 xx 5.3 xx 10^-11)/2`
= `1.6 xx 5.3 xx 10^-24`
= `8.48 xx 10^-24` Am2
From formula (ii),
L = `9.1 xx 10^-31 xx 2 xx 10^6 xx 5.3 xx 10^-11`
= `96.46 xx 10^-36`
∴ L ≈ `underline(9.646 xx 10^-35)` kgm2/s
- Orbital magnetic moment is `8.48 xx 10^-24` Am2.
- Angular momentum of electron is `9.646 xx 10^-35` kgm2/s.
APPEARS IN
संबंधित प्रश्न
Obtain an expression for the orbital magnetic moment of an electron rotating about the nucleus in an atom.
What is stated in terms of Bohr magneton?
The electron in the hydrogen atom is moving with a speed of 2.5 × 106 m/s in an orbit of a radius of 0.5 Å. What is the Magnetic moment of the revolving electron?
Explain the origin of magnetism in material, hence find a magnetic moment of an electron revolving around the nucleus of an atom.
If M0 and L0 denote the orbital angular moment and the angular momentum of the electron due to its orbital motion, then the gyromagnetic ratio is given by ______
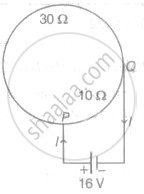
A circular coil of radius R has a resistance of 40 Ω. Figure shows two points P and Q on the circumference separated by a distance `(pi"R")/2`, which are connected to a 16 V battery with internal resistance of 0.5 Ω. What is the value of current I flowing through the circuit?
The magnetic moment of electrons due to orbital motion is proportional to ______.
(n = principal quantum numbers)
The S.I. unit of gyromagnetic ratio is ______
The Gyromagnetic ratio of the electron revolving in a circular orbit of a hydrogen atom is 8.8 x 1010 C kg-1. What is the mass of the electron? (Given charge of the electron = 1.6 x 10-19 C.)
The angle made by orbital angular momentum of electron with the direction of the orbital magnetic moment is ______.
An electron revolving in a circular orbit of radius 'r' with velocity 'v' and frequency v has orbital magnetic moment 'M'. If the frequency of revolution is tripled then the new magnetic moment will be ____________.
The electron in the hydrogen atom is moving with a speed of 1.5 x 106 m/s in an orbit of radius 2 Å. Magnetic moment of the revolving electron is ____________.
Which one of the following proportionality represents the relation between orbital magnetic moment M0 and orbital angular momentum L0 of an electron?
An electron revolving in a circular orbit of radius 'r' with velocity 'V' and frequency 'v' has orbital magnetic moment 'M'. If the frequency of revolution is doubled then the new magnetic moment will be ____________.
Magnetic moment of revolving electron of charge 'e' and mass 'm' in terms of angular momentum 'L' of electron is ____________.
An electron in the ground state of hydrogen atom is revolving in a circular orbit of radius R. The orbital magnetic moment of the electron is ____________. (m = mass of electron, h = Planck's constant, e = electronic charge)
In an atom, electron of charge (-e) perform U.C.M. around a stationary positively charged nucleus, with period of revolution 'T'. If 'r' is the radius of the orbit of the electron and 'v' is the orbital velocity, then the circulating current (I) is proportional to ____________.
Which of the following expression represents the relation between orbital magnetic moment and orbital angular momentum of an electron?
An electron in an atom is revolving around the nucleus in a circular orbit of radius 0.53 A, with a speed of 2 x 106 m/s. Find the resultant orbital magnetic moment and angular momentum of electron.(e = 1.6 x 10-19 C, m = 9.1 x 10-31 kg)
The electron in the hydrogen atom is moving with a speed at 2.3 x 106 m/s in an orbit of radius 0.53Å. Calculate the magnetic moment of the revolving electron.
