Advertisements
Advertisements
प्रश्न
An electron moving along positive X axis with a velocity of 8 ×107ms-1 enters a region having uniform magnetic field B = 1.3 × 10-3 T along positive Y axis.
- Explain why the electron describes a circular path.
- Calculate the radius of the circular path described by the electron.
उत्तर
(a) Because force exerted by the magnetic field is always perpendicular to its velocity. So, it provides the necessary centripetal force to the electron.
(b) `"e"/"m" = "v"/("Br")`
`(1.6 xx 10^(-19))/(9.1 xx 10^(-31)) = (8 xx 10 xx 7)/(1.3 xx 10^(-3) xx "r")`
∴ r = 0.35 m
APPEARS IN
संबंधित प्रश्न
Draw a neat and labelled diagram of suspended coil type moving coil galvanometer.
Two identical circular loops, P and Q, each of radius r and carrying equal currents are
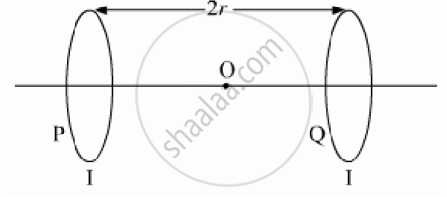
kept in the parallel planes having a common axis passing through O. The direction of current in P is clockwise and in Q is anti-clockwise as seen from O which is equidistant from the loops P and Q. Find the magnitude of the net magnetic field at O.
Write the expression for the magnetic moment `vecm`due to a planar square loop of side ‘l’ carrying a steady current I in a vector form.
In the given figure this loop is placed in a horizontal plane near a long straight conductor carrying a steady current I1 at a distance l as shown. Give reason to explain that the loop will experience a net force but no torque. Write the expression for this force acting on the loop.

A current loop of arbitrary shape lies in a uniform magnetic field B. Show that the net magnetic force acting on the loop is zero.
A circular loop of one turn carries a current of 5.00 A. If the magnetic field B at the centre is 0.200 mT, find the radius of the loop.
If the net magnetic force acting on a loop is zero then ____________.
If number of turns in moving coil galvanometer becomes half, then the deflection for the same current will become ____________.
What is the magnetic moment of a current-carrying circular coil if the radius of the circular coil is 'R' and magnetic induction at the center is 'B'?
A uniform conducting wire of length 12a and resistance R is wound up as a current-carrying coil in the shape of (i) an equilateral triangle of side a; (ii) a square of sides a and, (iii) a regular hexagon of sides a. The coil is connected to a voltage source V0. Find the magnetic moment of the coils in each case.
A rectangular coil of 10 turns, each of area 0.05 m2, is suspended freely in a radial magnetic field of 0.01 T. If the torsional constant of the suspension fibre is 5 × 10−9 N·m per degree, find the angle through which the coil rotates when a current of 30 μA is passed through it.
