Advertisements
Advertisements
प्रश्न
Two identical circular loops, P and Q, each of radius r and carrying equal currents are
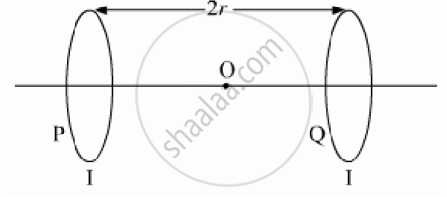
kept in the parallel planes having a common axis passing through O. The direction of current in P is clockwise and in Q is anti-clockwise as seen from O which is equidistant from the loops P and Q. Find the magnitude of the net magnetic field at O.
उत्तर
The standard formula for field at an axial point is given as
`B=(mu_0ia^2)/(2(a^2 +d^2)^(2/3))`
So, in this case
`B = (mu_0Ir^2)/(2(r^2 +((2r)/2)^2)^(3/2)) = (mu_0I)/((2)^(5/2)r)`
Now, as the current flowing in loop P is clockwise by using right hand thumb’s rule the direction of the magnetic field will be towards left and as the current in loop Q is clockwise then the direction of magnetic field is towards left. So the net magnetic field at point O will be the sum of the magnetic fields due to loops P and Q.
Also, as the fields produced are at an equal distance to O, BP = BQ,
So, net field
`B=B_P+B_Q= 2(mu_0I)/((2)^(5/3)r) = (mu_0I)/((2)^(3/2)r)`
संबंधित प्रश्न
Draw a neat and labelled diagram of suspended coil type moving coil galvanometer.
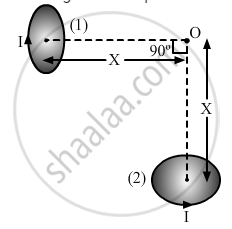
Two very small identical circular loops, (1) and (2), carrying equal currents I are placed vertically (with respect to the plane of the paper) with their geometrical axes perpendicular to each other as shown in the figure. Find the magnitude and direction of the net magnetic field produced at the point O.
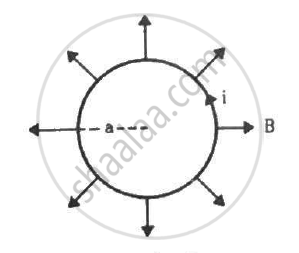
A circular loop of radius a, carrying a current i, is placed in a two-dimensional magnetic field. The centre of the loop coincides with the centre of the field (figure). The strength of the magnetic field at the periphery of the loop is B. Find the magnetic force on the wire.
Derive the expression for the torque on a current-carrying coil in a magnetic field.
A rectangular coil of length 0.12 m and width 0.1 m having 100 turns of wire is suspended vertically in a uniform magnetic field of strength 0.4 Wb/m2. The coil carries a current of 2.5 A. If the plane of the coil is inclined at an angle of 30° with the direction of the field, the torque required to keep the coil in stable equilibrium will be ____________.
A 100 turn rectangular coil measuring 0.02 m x 0.06 m of an ammeter is in a magnetic field of induction 0.4 tesla. The torsional constant of the suspension fibre is 5 x 10-7 newton x metre/degree. The maximum reading of the ammeter corresponds to a deflection of the coil through 30°. If the magnetic field is radial, then the maximum current that can be measured with this ammeter is ____________.
The sensitivity of moving coil galvanometer is inversely proportional to ____________.
A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, what is the
(a) total torque on the coil,
(b) total force on the coil,
(c) average force on each electron in the coil due to the magnetic field?
(The coil is made of copper wire of cross-sectional area 10–5 m2, and the free electron density in copper is given to be about 1029 m–3.)
Calculate the orbital magnetic dipole moment of the electron in the second Bohr orbit of the hydrogen atom, given the radius of the orbit is 2.1 Å and the orbital speed is 1.1 × 106 m/s.
A rectangular coil of 10 turns, each of area 0.05 m2, is suspended freely in a radial magnetic field of 0.01 T. If the torsional constant of the suspension fibre is 5 × 10−9 N·m per degree, find the angle through which the coil rotates when a current of 30 μA is passed through it.
