Advertisements
Advertisements
प्रश्न
Derive the expression for the torque on a current-carrying coil in a magnetic field.
उत्तर
Consider a rectangular loop PQRS carrying current I is placed in a uniform magnetic field B. Let a and b be the length and breadth rectangular loop respectively. The unit vector n̂ normal to the plane of the loop makes an angle θ with the magnetic field.

Rectangular coil placed in a magnetic field
- The magnitude of the magnetic force acting on the current-carrying arm PQ is FPQ = IaBsin (π/2) = IaB.
- The magnitude of the force on the arm QR is FQR =IbBsin `(pi/2 - theta)` = lbB cos θ and its direction.
- The magnitude of the force on the arm RS is FRS =IaBsin (π/2) = IaB and its direction is downwards.
- The magnitude of the force acting on the arm SP is FSP = lbB`(pi/2 - theta)` = lbB cos θ and its direction.
- Since the forces FQR and FSP are equal, opposite, and collinear, they cancel each other. But the forces FPQ and FRS.
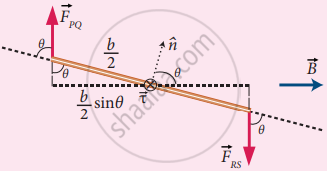
Side view of current loop - The magnitude of torque acting on the arm PQ about AB is τPQ = (1/2 sinθ) and points in the direction of AB. The magnitude of the torque acting on the arm. RS about AB is τRS = (b/2 sinθ) IaB and points also in the same direction AB.
- The total torque acting on the entire loop about an axis AB is given by
`tau = ("b"/2 sin theta) "F"_"PQ" + ("b"/2 sin theta) "F"_"RS"`
= Ia(bsinθ)B
τ = IABsinθ along the direction B.
In vector form,
`vec tau= (vec"IA") xx vec"B"`. - The above equation can also be written in terms of magnetic dipole moment.
`vectau` = \[\overrightarrow{\mathrm{pm}}\] × \[\overrightarrow{\mathrm{B}}\] where \[\overrightarrow{\mathrm{pm}}\] = \[\overrightarrow{\mathrm{IA}}\] - If there are N turns in the rectangular loop, the torque is given by
τ = NIAB sinθ
Special cases:
- When θ =90° or the plane of the loop is parallel to the magnetic field, the torque on the current loop is maximum.
τmax = IAB - When θ = 0°/180° or the plane of the loop is perpendicular to the magnetic field, the torque on the current loop is zero.
APPEARS IN
संबंधित प्रश्न
Will a current loop placed in a magnetic field always experience a zero force?
A rectangular wire-loop of width a is suspended from the insulated pan of a spring balance, as shown in the figure. A current i exists in the anti-clockwise direction in the loop. A magnetic field B exists in the lower region. Find the change in the tension of the spring if the current in the loop is reversed.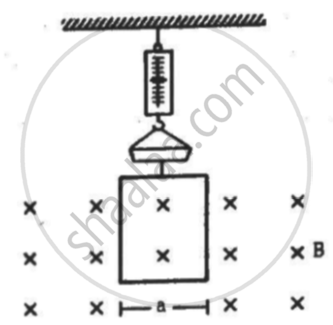
Suppose that the radius of cross-section of the wire used in the previous problem is r. Find the increase in the radius of the loop if the magnetic field is switched off. Young's modulus of the material of the wire is Y.
A circular loop of one turn carries a current of 5.00 A. If the magnetic field B at the centre is 0.200 mT, find the radius of the loop.
Derive the expression for the torque acting on a current-carrying loop placed in a magnetic field.
A Rectangular coil of 10 turns, each of area 0.05 m2, is suspended freely in a uniform magnetic field of induction 0.01 T. A current of 30 µA is passed through it.
(i) What is the magnetic moment of the coil?
(ii) What is the maximum torque experienced by the coil?
Derive an expression for the net torque on a rectangular current carrying loop placed in a uniform magnetic field with its rotational axis perpendicular to the field.
If the net magnetic force acting on a loop is zero then ____________.
What is the magnetic moment of a current-carrying circular coil if the radius of the circular coil is 'R' and magnetic induction at the center is 'B'?
A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, what is the
(a) total torque on the coil,
(b) total force on the coil,
(c) average force on each electron in the coil due to the magnetic field?
(The coil is made of copper wire of cross-sectional area 10–5 m2, and the free electron density in copper is given to be about 1029 m–3.)
