Advertisements
Advertisements
Question
Derive the expression for the torque on a current-carrying coil in a magnetic field.
Solution
Consider a rectangular loop PQRS carrying current I is placed in a uniform magnetic field B. Let a and b be the length and breadth rectangular loop respectively. The unit vector n̂ normal to the plane of the loop makes an angle θ with the magnetic field.

Rectangular coil placed in a magnetic field
- The magnitude of the magnetic force acting on the current-carrying arm PQ is FPQ = IaBsin (π/2) = IaB.
- The magnitude of the force on the arm QR is FQR =IbBsin `(pi/2 - theta)` = lbB cos θ and its direction.
- The magnitude of the force on the arm RS is FRS =IaBsin (π/2) = IaB and its direction is downwards.
- The magnitude of the force acting on the arm SP is FSP = lbB`(pi/2 - theta)` = lbB cos θ and its direction.
- Since the forces FQR and FSP are equal, opposite, and collinear, they cancel each other. But the forces FPQ and FRS.
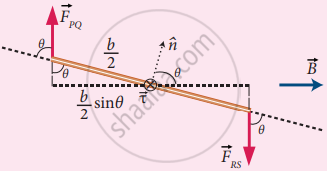
Side view of current loop - The magnitude of torque acting on the arm PQ about AB is τPQ = (1/2 sinθ) and points in the direction of AB. The magnitude of the torque acting on the arm. RS about AB is τRS = (b/2 sinθ) IaB and points also in the same direction AB.
- The total torque acting on the entire loop about an axis AB is given by
`tau = ("b"/2 sin theta) "F"_"PQ" + ("b"/2 sin theta) "F"_"RS"`
= Ia(bsinθ)B
τ = IABsinθ along the direction B.
In vector form,
`vec tau= (vec"IA") xx vec"B"`. - The above equation can also be written in terms of magnetic dipole moment.
`vectau` = \[\overrightarrow{\mathrm{pm}}\] × \[\overrightarrow{\mathrm{B}}\] where \[\overrightarrow{\mathrm{pm}}\] = \[\overrightarrow{\mathrm{IA}}\] - If there are N turns in the rectangular loop, the torque is given by
τ = NIAB sinθ
Special cases:
- When θ =90° or the plane of the loop is parallel to the magnetic field, the torque on the current loop is maximum.
τmax = IAB - When θ = 0°/180° or the plane of the loop is perpendicular to the magnetic field, the torque on the current loop is zero.
APPEARS IN
RELATED QUESTIONS
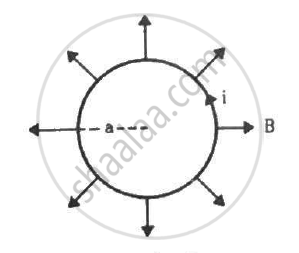
A circular loop of radius a, carrying a current i, is placed in a two-dimensional magnetic field. The centre of the loop coincides with the centre of the field (figure). The strength of the magnetic field at the periphery of the loop is B. Find the magnetic force on the wire.
A Rectangular coil of 10 turns, each of area 0.05 m2, is suspended freely in a uniform magnetic field of induction 0.01 T. A current of 30 µA is passed through it.
(i) What is the magnetic moment of the coil?
(ii) What is the maximum torque experienced by the coil?
Derive an expression for the net torque on a rectangular current carrying loop placed in a uniform magnetic field with its rotational axis perpendicular to the field.
A small cylindrical soft iron piece is kept in a galvanometer so that
If in a moving coil galvanometer, a current I produces a deflection `theta,` then ____________.
Two galvanometers 'G1' and 'G2' require 2 mA and 3 mA respectively to produce the same deflection. Then _______.
The sensitivity of moving coil galvanometer is inversely proportional to ____________.
A current of 10 A is flowing in a wire of length 1.5 m. A force of 15 N acts on it when it is placed in a uniform magnetic field of 2 T. The angle between the magnetic field and the direction of the current is ______.
A thin flexible wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is ______.


An electron moving along positive X axis with a velocity of 8 ×107ms-1 enters a region having uniform magnetic field B = 1.3 × 10-3 T along positive Y axis.
- Explain why the electron describes a circular path.
- Calculate the radius of the circular path described by the electron.
