Advertisements
Advertisements
प्रश्न
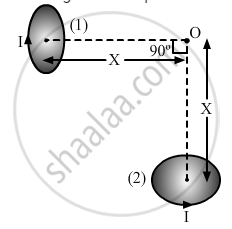
Two very small identical circular loops, (1) and (2), carrying equal currents I are placed vertically (with respect to the plane of the paper) with their geometrical axes perpendicular to each other as shown in the figure. Find the magnitude and direction of the net magnetic field produced at the point O.
उत्तर
The magnetic field at a point due to a circular loop is given by
a = radius of the loop
r = distance of O from the centre of the loop
Since I , a and r = x are the same for both the loops, the magnitude of B will be the same and is given by
\[B_1 = B_2 = \frac{\mu_0}{4\pi} . \frac{2\pi I a^2}{\left( a^2 + x^2 \right)^{3/2}} \]
The direction of magnetic field due to loop (1) will be away from O and that of the magnetic field due to loop (2) will be towards O as shown. The direction of the net magnetic field will be as shown below:
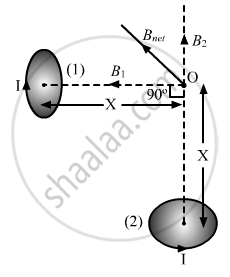
The magnitude of the net magnetic field is given by
\[B_{net} = \sqrt{{B_1}^2 + {B_2}^2}\]
\[ \Rightarrow B_{net} = \frac{\mu_0}{4\pi} . \frac{2\sqrt{2}\pi I a^2}{\left( a^2 + x^2 \right)^{3/2}}\]
संबंधित प्रश्न
A rectangular wire-loop of width a is suspended from the insulated pan of a spring balance, as shown in the figure. A current i exists in the anti-clockwise direction in the loop. A magnetic field B exists in the lower region. Find the change in the tension of the spring if the current in the loop is reversed.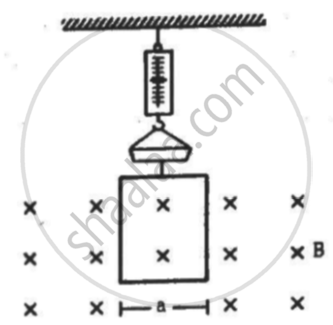
A current loop of arbitrary shape lies in a uniform magnetic field B. Show that the net magnetic force acting on the loop is zero.
A circular loop of one turn carries a current of 5.00 A. If the magnetic field B at the centre is 0.200 mT, find the radius of the loop.
Derive the expression for the torque acting on a current-carrying loop placed in a magnetic field.
A Rectangular coil of 10 turns, each of area 0.05 m2, is suspended freely in a uniform magnetic field of induction 0.01 T. A current of 30 µA is passed through it.
(i) What is the magnetic moment of the coil?
(ii) What is the maximum torque experienced by the coil?
Derive an expression for the net torque on a rectangular current carrying loop placed in a uniform magnetic field with its rotational axis perpendicular to the field.
The magnetic field developed due to current carrying coil at its centre is 'B'. If the new coil of two turns is prepared from the above coil and same current is passed, then the magnetic field at the centre of the new coil will be ____________.
A circular coil of 20 turns and radius 10 cm is placed in a uniform magnetic field of 0.10 T normal to the plane of the coil. If the current in the coil is 5.0 A, what is the
(a) total torque on the coil,
(b) total force on the coil,
(c) average force on each electron in the coil due to the magnetic field?
(The coil is made of copper wire of cross-sectional area 10–5 m2, and the free electron density in copper is given to be about 1029 m–3.)
A thin flexible wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is ______.


A rectangular coil of 10 turns, each of area 0.05 m2, is suspended freely in a radial magnetic field of 0.01 T. If the torsional constant of the suspension fibre is 5 × 10−9 N·m per degree, find the angle through which the coil rotates when a current of 30 μA is passed through it.
