Advertisements
Advertisements
Question
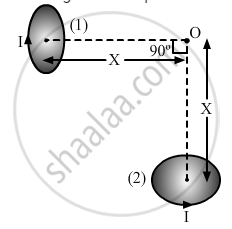
Two very small identical circular loops, (1) and (2), carrying equal currents I are placed vertically (with respect to the plane of the paper) with their geometrical axes perpendicular to each other as shown in the figure. Find the magnitude and direction of the net magnetic field produced at the point O.
Solution
The magnetic field at a point due to a circular loop is given by
a = radius of the loop
r = distance of O from the centre of the loop
Since I , a and r = x are the same for both the loops, the magnitude of B will be the same and is given by
\[B_1 = B_2 = \frac{\mu_0}{4\pi} . \frac{2\pi I a^2}{\left( a^2 + x^2 \right)^{3/2}} \]
The direction of magnetic field due to loop (1) will be away from O and that of the magnetic field due to loop (2) will be towards O as shown. The direction of the net magnetic field will be as shown below:
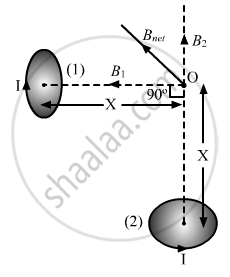
The magnitude of the net magnetic field is given by
\[B_{net} = \sqrt{{B_1}^2 + {B_2}^2}\]
\[ \Rightarrow B_{net} = \frac{\mu_0}{4\pi} . \frac{2\sqrt{2}\pi I a^2}{\left( a^2 + x^2 \right)^{3/2}}\]
RELATED QUESTIONS
Write the expression for the magnetic moment `vecm`due to a planar square loop of side ‘l’ carrying a steady current I in a vector form.
In the given figure this loop is placed in a horizontal plane near a long straight conductor carrying a steady current I1 at a distance l as shown. Give reason to explain that the loop will experience a net force but no torque. Write the expression for this force acting on the loop.

The torque on a current loop is zero if the angle between the positive normal and the magnetic field is either θ = 0 or θ = 180°. In which of the two orientations, the equilibrium is stable?
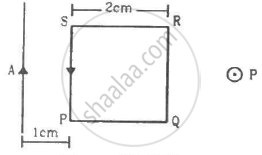
A square loop PQRS carrying a current of 6.0 A is placed near a long wire carrying 10 A as shown in figure. (a) Show that the magnetic force acting on the part PQ is equal and opposite to the part RS. (b) Find the magnetic force on the square loop.
Derive the expression for the torque acting on a current-carrying loop placed in a magnetic field.
A rectangular coil of length 0.12 m and width 0.1 m having 100 turns of wire is suspended vertically in a uniform magnetic field of strength 0.4 Wb/m2. The coil carries a current of 2.5 A. If the plane of the coil is inclined at an angle of 30° with the direction of the field, the torque required to keep the coil in stable equilibrium will be ____________.
A 100 turn rectangular coil measuring 0.02 m x 0.06 m of an ammeter is in a magnetic field of induction 0.4 tesla. The torsional constant of the suspension fibre is 5 x 10-7 newton x metre/degree. The maximum reading of the ammeter corresponds to a deflection of the coil through 30°. If the magnetic field is radial, then the maximum current that can be measured with this ammeter is ____________.
If in a moving coil galvanometer, a current I produces a deflection `theta,` then ____________.
Two galvanometers 'G1' and 'G2' require 2 mA and 3 mA respectively to produce the same deflection. Then _______.
The sensitivity of moving coil galvanometer is inversely proportional to ____________.
A circular coil having N turns of radius R carrying a current I is used to produce a magnetic field B at its centre O.
If this coil is opened and rewound such that the radius of the newly formed coil is 2R, carrying the same current I, what will be the magnetic field at the centre O?
