Advertisements
Advertisements
प्रश्न
An oil funnel of the tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of a cone. If the total height is 22 cm, the diameter of the cylindrical portion by 8 cm and the diameter of the top of the funnel be 18 cm, then find the area of the tin sheet required to make the funnel.
उत्तर
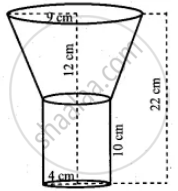
Total height of oil funnel = 22 cm
Height of the cylindrical portion = 10 cm
Height of the frustum (h) = 22 – 10 = 12 cm
Radius of the cylindrical portion = 4 cm
Radius of the bottom of the frustum = 4 cm
Top radius of the funnel (frustum) = `18/2` = 9 cm
Area of the tin sheet required = C.S.A of the frustum + C.S.A of the cylinder
= π (R + r) l + 2πrh sq.units.
= `[pi(9 + 4) sqrt(12^2 + (9 - 4)^2) + 2pi xx 4 xx 10]"cm"^2`
= `pi[13 xx sqrt(144 + 25) + 25 + 80]"cm"^2`
= `22/7 [13 xx 13 + 80] "cm"^2`
= `22/7 [169 + 80] "cm"^2`
= `22/7 xx 249 "cm"^2`
= 782.57 cm2
Area of sheet required to make the funnel = 782.57 cm2
APPEARS IN
संबंधित प्रश्न
A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained is drawn into a wire of diameter 1/16 cm, find the length of the wire [use π=22/7]
The circumferences of circular faces of a frustum are 132 cm and 88 cm and its height is 24 cm. To find the curved surface area of the frustum complete the following activity.( \[\pi = \frac{22}{7}\])
A milk container of height 16 cm is made of metal sheet in the form of a frustum of a cone with radii of its lower and upper ends as 8 cm and 20 cm respectively . Find the cost of milk at the rate of ₹44 per litre which the container can hold.
A hemisphere of lead of radius 7 cm is cast into a right circular cone of height 49 cm. Find the radius of the base.
The surface area of a sphere is the same as the curved surface area of a cone having the radius of the base as 120 cm and height 160 cm. Find the radius of the sphere.
The slant height of the frustum of a cone is 5 cm. If the difference between the radii of its two circular ends is 4 cm, write the height of the frustum.
The height of a right circular cone is 20 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume be `1/8` of the volume of the given cone, then at what height above the base is the section made?
The radii of the circular ends of a frustum of height 6 cm are 14 cm and 6 cm, respectively. Find the slant height of the frustum.
Choose the correct answer of the following question:
If the height of a bucket in the shape of frustum of a cone is 16 cm and the diameters of its two circular ends are 40 cm and 16 cm, then its slant height is
