Advertisements
Advertisements
प्रश्न
Answer carefully, with reason:
If the potential energy of two billiard balls depends only on the separation distance between their centres, is the collision elastic or inelastic? (Note, we are talking here of potential energy corresponding to the force during collision, not gravitational potential energy.)
उत्तर
The potential energy depends on the separation distance between centres; this means that during the collision, the force acting between the bodies is conservative; therefore, energy will be conserved. Thus, the collision will be elastic.
APPEARS IN
संबंधित प्रश्न
Solve the following problem.
A marble of mass 2m travelling at 6 cm/s is directly followed by another marble of mass m with double speed. After a collision, the heavier one travels with the average initial speed of the two. Calculate the coefficient of restitution.
Explain the characteristics of elastic and inelastic collision.
A ball moving with velocity 5 m/s collides head on with another stationary ball of double mass. If the coefficient of restitution is 0.8, then their velocities (in m/s) after collision will be ____________.
A particle of mass 'm' collides with another stationary particle of mass 'M'. A particle of mass 'm' stops just after collision. The coefficient of restitution is ______.
A block of mass 'm' moving along a straight line with constant velocity `3vec"v"` collides with another block of same mass at rest. They stick together and move with common velocity. The common velocity is ______.
A body of mas 'm' moving with speed 3 m/s collides with a body of mass '2m' at rest. The coalesced mass will start to move with a speed of ______.
Consider a one-dimensional motion of a particle with total energy E. There are four regions A, B, C and D in which the relation between potential energy V, kinetic energy (K) and total energy E is as given below:
Region A : V > E
Region B : V < E
Region C : K > E
Region D : V > K
State with reason in each case whether a particle can be found in the given region or not.
The bob A of a pendulum released from horizontal to the vertical hits another bob B of the same mass at rest on a table as shown in figure.
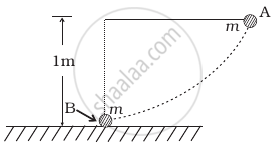
If the length of the pendulum is 1 m, calculate
- the height to which bob A will rise after collision.
- the speed with which bob B starts moving. Neglect the size of the bobs and assume the collision to be elastic.
A particle of mass m with an initial velocity u`hat"i"` collides perfectly elastically with a mass 3m at rest. It moves with a velocity v`hat"j"` after collision, then, v is given by :
An alpha-particle of mass m suffers 1-dimensional elastic collision with a nucleus at rest of unknown mass. It is scattered directly backwards losing, 64% of its initial kinetic energy. The mass of the nucleus is ______.
