Advertisements
Advertisements
प्रश्न
बिन्दु (0, 0, -a) तथा (0, 0, a) पर दो आवेश क्रमशः -q और +q स्थित हैं।
- बिन्दुओं (0, 0, z) और (x, y, 0) पर स्थिरविद्युत विभव क्या है?
- मूल बिन्दु से किसी बिन्दु की दूरी पर विभव की निर्भरता ज्ञात कीजिए, जबकि \[\frac{r}{a}\] >> 1
- x-अक्ष पर बिन्दु (5, 0, 0) से बिन्दु (-7, 0, 0) तक एक परीक्षण आवेश को ले जाने में कितना कार्य करना होगा? यदि परीक्षण आवेश को उन्हीं बिन्दुओं के बीच x-अक्ष से होकर न ले जाएँ तो क्या उत्तर बदल जाएगा?
उत्तर
दिए गए बिन्दु आवेश एक विद्युत द्विध्रुव बनाते हैं।
आवेशों के बीच की दूरी = 2a
∴ विद्युत द्विध्रुव आघूर्ण `vec"p" = "q" xx 2vec"a"`
= `2"q"vec"a"`
(a) बिन्दु (0, 0, z) द्विध्रुव की अक्ष पर स्थित है,
∴ इस बिन्दु पर विद्युत विभव V = `+- 1/(4piepsilon_0) * "p"/("z"^2 - "a"^2)`
बिन्दु (x, y, 0) द्विध्रुव के विषुवत तल में स्थित है; अतः इस बिन्दु पर विद्युत विभव शून्य होगा।
(b)
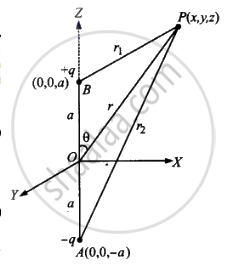
द्विध्रुव के कारण किसी बिन्दु पर विद्युत विभव:
माना कोई बिन्दु P, द्विध्रुव के केन्द्र (मूल बिन्दु) से r दूरी पर स्थित है। इस बिन्दु की बिन्दु आवेशों + q तथा - q से दूरियाँ क्रमशः r1 तथा r2 हैं।
तब बिन्दु P पर द्विध्रुव के कारण विद्युत विभव
V = `1/(4piepsilon_0) ("q"/"r"_1 - "q"/"r"_2)` ...(1)
माना ∠ZOP = θ तथा
Δ OBP में,
`"r"_1^2 = "r"^2 + "a"^2 - 2"ar" cos theta` ...(2)
तथा Δ AOP में,
`"r"_2^2 = "r"^2 + "a"^2 - 2"ar" cos (180^circ - theta)`
या `"r"_2^2 = "r"^2 + "a"^2 + 2"ar" cos theta` ...(3)
∴ समीकरण (2) से,
`"r"_1^2 = "r"^2(1 - "2a"/"r" cos theta + "a"^2/"r"^2)`
`~~ "r"^2 (1 - "2a"/"r" cos theta) ...["r"/"a" ">>" 1 "मानते हुए" "a"/"r" "के द्विघात पद छोड़ने पर"]`
इसी प्रकार `"r"_2^2 ~~ "r"^2 (1 + "2a"/"r" cos theta)`
`∴ 1/"r"_1 ~~ 1/"r"(1 + "2a"/"r" cos theta)^(-1//2)`
या `1/"r"_1 ~~ 1/"r"(1 + "a"/"r" cos theta)` (द्विपद प्रमेय से)
इसी प्रकार `1/"r"_1 ~~ 1/"r"(1 - "a"/"r" cos theta)`
∴ समीकरण (1) में मान रखने पर,
V = `1/(4piepsilon_0) "q"/"r" xx "2a"/"r" cos theta`
`= 1/(4piepsilon_0) ((2"qa")cos theta)/"r"^2`
अतः द्विध्रुव के कारण उसके केन्द्र से r दूरी पर `("r"/"a" > > 1)` विद्युत विभव
V = `("p" cos theta)/(4 piepsilon_0"r"^2)` जहाँ p = 2qa
परन्तु `"p" cos theta = vec"p" * hat"r"` जहाँ `hat"r", vec"r"` की दिशा में एक सदिश है।
∴ V = `(vec"p" * hat"r")/(4 piepsilon_0"r"^2)`
(c) बिन्दु P (5, 0, 0) तथा Q(-7, 0, 0) द्विध्रुव के विषुवत तल में स्थित है; अतः इन दोनों बिन्दुओ पर विभव शुन्य होगा।
∴ परीक्षण आवेश q0 को बिन्दु P से Q तक ले जाने में किया गया कार्य
W = q0 [V(Q) - V(P)] = 0 [V(P) = V(Q) = 0]
विद्युत क्षेत्र एक संरक्षी क्षेत्र है जिसमें किया गया कार्य केवल अन्त्य बिन्दुओं पर निर्भर करता है, न की मार्ग पर।
अतः उत्तर ,में कोई परिवर्तन नहीं आएगा।
APPEARS IN
संबंधित प्रश्न
दो बड़े चालक गोले जिन पर आवेश Q1 और Q2 हैं, एक-दूसरे के समीप लाए जाते हैं। क्या इनके बीच स्थिर विद्युत बल का परिमाण तथ्यत:
Q1Q2/4πε0r2
द्वारा दर्शाया जाता है, जहाँ r इनके केन्द्रों के बीच की दूरी है?
यदि कूलॉम के नियम में `1//"r"^3` निर्भरता का समावेश (`1//"r"^2` के स्थान पर) हो तो क्या गाउस का नियम अभी भी सत्य होगा?
स्थिरविद्युत-क्षेत्र विन्यास में एक छोटा परीक्षण आवेश किसी बिन्दु पर विराम में छोड़ा जाता है। क्या यह उस बिन्दु से होकर जाने वाली क्षेत्र रेखा के अनुदिश चलेगा?
