Advertisements
Advertisements
प्रश्न
बिंदु P, Q, R और S के कारण रेखाखंड AB पाँच सर्वांगसम भागों में विभाजित होता है। यदि A-P-Q – R-S-B और Q(12, 14) तथा S(4, 18) हो तो A, P, R, B के निर्देशांक ज्ञात कीजिए।
उत्तर
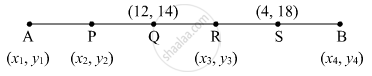
Q(12, 14) और S(4, 18).
मानो कि, A(x1, y1); P(x2, y2); R(x3, y3) और B(x4, y4)
बिंदु Q यह रेख AS का मध्यबिंदु है |
∴ मध्यबिंदु के सूत्र से,
`12 = (x_1 + 4)/2`
∴ x1 + 4 = 12 × 2
∴ x1 + 4 = 24
∴ x1 = 24 - 4
∴ x1 = 20
`14 = (y_1 + 18)/2`
∴ `y_1 + 18 = 14 xx 2`
∴ `y_1 + 18 = 28`
∴ `y_1 = 28 - 18`
∴ `y_1 = 10`
बिंदु A का निर्देशांक (20, 10) है |
बिंदु P यह रेख AQ का मध्यबिंदु है |
∴ मध्यबिंदु के सूत्र से,
`x_2 = (20 + 12)/2`
∴ `x_2 = 32/2`
∴ `x_2 = 16`
`y_2 = (10 + 14)/2`
∴ `y_2 = 24/2`
∴ `y_2 = 12`
∴ बिंदु P का निर्देशांक (16, 12) है |
बिंदु R यह रेख QS का मध्यबिंदु है |
∴ मध्यबिंदु के सूत्र से,
`x_3 = (12 + 4)/2`
∴ `x_3 = 16/2`
∴ `x_3 = 8`
`y_3 = (14 + 18)/2`
∴ `y_3 = 32/2`
∴ `y_3 = 16`
∴ बिंदु R का निर्देशांक (8, 16) है |
बिंदु S यह रेख RB का मध्यबिंदु है |
∴ मध्यबिंदु के सूत्र से,
`4 = (8 + x_4)/2`
∴ `8 + x_4 = 4 xx 2`
∴ `8 + x_4 = 8`
∴ `x_4 = 8 - 8`
∴ `x_4 = 0`.
`18 = (16 + y_4)/2`
∴ `16 + y_4 = 18 xx 2`
∴ `16 + y_4 = 36`
∴ `y_4 = 36 - 16`
∴ `y_4 = 20`
∴ बिंदु B का निर्देशांक (0, 20) है |
बिंदु A का निर्देशांक (20, 10); बिंदु P का निर्देशांक (16, 12); बिंदु R का निर्देशांक (8, 16) तथा बिंदु B का निर्देशांक (0, 20) है |
APPEARS IN
संबंधित प्रश्न
रेखाखंड AB यह वृत्त का व्यास है, जिसका केंद्र बिंदु P है। A(2, -3) और P(-2, 0) हो तो बिंदु B के निर्देशांक ज्ञात कीजिए।
(22, 20) और (0, 16) को जोड़ने वाले रेखाखंड के मध्यबिंदु के निर्देशांक ज्ञात कीजिए।
P(0, 6) और Q(12, 20) इन बिंदुओं को जोड़ने वाले रेखाखंड के मध्य बिंदु का निर्देशांक ज्ञात कीजिए।
A(-1, 1), B(5, -3) और C(3, 5) इन शीर्ष बिंदु वाले त्रिभुज की माध्यिकाओं की लंबाई ज्ञात कीजिए।
बिन्दु P के निर्देशांक ज्ञात कीजिए, यदि बिन्दु P रेखाखंड AB का मध्य बिन्दु है, जिसमें A(-4, 2) व B(6, 2) हो।
हल:
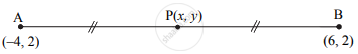
माना (-4, 2) = (x1, y1) तथा (6, 2) = (x2, y2) और बिन्दु P के निर्देशांक (x, y) हैं।
मध्यबिन्दु के सूत्रनुसार,
`x = (x_1 + x_2)/2`
∴ `x = (square + 6)/2`
∴ `x = square/2`
∴ x = `square`
`y = (y_1 + y_2)/2`
∴ `y = (2 + square)/2`
∴ y = `4/2`
∴ y = `square`
∴ मध्यबिन्दु P के निर्देशांक `square` हैं।
