Advertisements
Advertisements
प्रश्न
Calculate the energy required for the process
\[\ce{He^+_{(g)} -> He^{2+}_{(g)} + e^-}\]
The ionization energy for the H atom in the ground state is 2.18 ×10–18 J atom–1
उत्तर
Energy associated with hydrogen-like species is given by,
`"E"_"n" = - 2.18 xx 10^(-18) ("Z"^2/"n"^2)"J"`
For ground state of hydrogen atom,
`triangle "E" = "E"_oo - "E"_1`
`= 0 - [-2.18 xx 10^(-18) {(1)^2/(1)^2}]`J
`triangle "E" =2.18 xx 10^(-18) "J"`
For the given process,
\[\ce{He^+_{(g)} -> He^{2+}_{(g)} + e^-}\]
An electron is removed from n = 1 to n = ∞.
`triangle "E" = "E"_oo - "E"_1`
`= 0-[-2.18 xx 10^(-18) {(2)^2/(1)^2}]`
`triangle "E" = 8.72 xx 10^(-18)` J
∴ The energy required for the process is `8.72 xx 10^(-18)`J
APPEARS IN
संबंधित प्रश्न
(i) State Bohr's quantization condition for defining stationary orbits. How does the de Broglie hypothesis explain the stationary orbits?
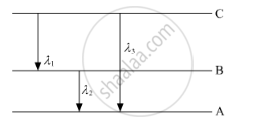
(ii) Find the relation between three wavelengths λ1, λ2 and λ3 from the energy-level diagram shown below.
Calculate the radius of Bohr’s fifth orbit for hydrogen atom
Explain, giving reasons, which of the following sets of quantum numbers are not possible.
(a) n = 0, l = 0, ml = 0, ms = + ½
(b) n = 1, l = 0, ml = 0, ms = – ½
(c) n = 1, l = 1, ml = 0, ms = + ½
(d) n = 2, l = 1, ml = 0, ms = – ½
(e) n = 3, l = 3, ml = –3, ms = + ½
(f) n = 3, l = 1, ml = 0, ms = + ½
(a) Using the Bohr’s model calculate the speed of the electron in a hydrogen atom in the n = 1, 2, and 3 levels.
(b) Calculate the orbital period in each of these levels.
Suppose, the electron in a hydrogen atom makes transition from n = 3 to n = 2 in 10−8 s. The order of the torque acting on the electron in this period, using the relation between torque and angular momentum as discussed in the chapter on rotational mechanics is
Calculate the magnetic dipole moment corresponding to the motion of the electron in the ground state of a hydrogen atom.
When a photon is emitted by a hydrogen atom, the photon carries a momentum with it. (a) Calculate the momentum carries by the photon when a hydrogen atom emits light of wavelength 656.3 nm. (b) With what speed does the atom recoil during this transition? Take the mass of the hydrogen atom = 1.67 × 10−27 kg. (c) Find the kinetic energy of recoil of the atom.
According to Bohr, 'Angular momentum of an orbiting electron is quantized'. What is meant by this statement?
If l3 and l2 represent angular momenta of an orbiting electron in III and II Bohr orbits respectively, then l3: l2 is :
Draw energy level diagram for a hydrogen atom, showing the first four energy levels corresponding to n=1, 2, 3 and 4. Show transitions responsible for:
(i) Absorption spectrum of Lyman series.
(ii) The emission spectrum of the Balmer series.
What is the energy in joules released when an electron moves from n = 2 to n = 1 level in a hydrogen atom?
In Bohr model of hydrogen atom, which of the following is quantised?
The energy of an electron in hth orbit of hydrogen atom is –13.6/n2ev energy required to excite the electron from the first orbit to the third orbit is
How will the energy of a hydrogen atom change if n increases from 1 to ∞?
The value of angular momentum for He+ ion in the first Bohr orbit is ______.
A hydrogen atom in is ground state absorbs 10.2 eV of energy. The angular momentum of electron of the hydrogen atom will increase by the value of ______.
(Given, Planck's constant = 6.6 × 10-34 Js)
A 20% efficient bulb emits light of wavelength 4000 Å. If the power of the bulb is 1 W, the number of photons emitted per second is ______.
[Take, h = 6.6 × 10-34 J-s]
The radius of the nth orbit in the Bohr model of hydrogen is proportional to ______.
How much is the angular momentum of an electron when it is orbiting in the second Bohr orbit of hydrogen atom?
The de Broglie wavelength of an electron in the first Bohr’s orbit of hydrogen atom is equal to ______.
