Advertisements
Advertisements
प्रश्न
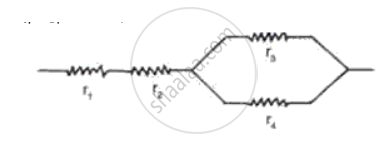
Calculate the equivalent resistance of the following combination of resistor r1, r2, r3, and r4
उत्तर १
In the given network, the series combination of resistors, r1 and r2 is connected in series with the parallel combination of resistors, r3 and r4
Equivalent resistance of resistor r1 and r2 , Rs= r1 + r2
Equivalent resistance of resistor r3 and r4 Rp = `[1/ "r"^3 + 1/"r"^4]^-1 = ("r"_3"r"_4)/("r"_3 + "r"_4)`
equivalent resistance of the given network, R = Rs + Rp = r1 + r2 + `("r"_3"r"_4)/("r"_3 + "r"_4)`
उत्तर २
Since r3 and r4 are in parallel
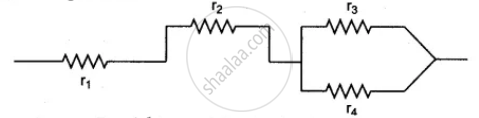
∴ Equivalent resistance R1 of this combination is given by
`1/"R"_1 = 1/"r"_3 + 1/"r"_4 = ("r"_4 + "r"_3)/("r"_4 "r"_3)`
or R1 = `("r"_3 "r"_4)/("r"_3 + "r"_4)`
Now r1, r2 and R1 are in series
∴ Equivalent resistance R of the whole combination is
R = r1 + r2 + `("r"_3 "r"_4)/("r"_3 + "r"_4)`
= `(("r"_1 + "r"_2)("r"_3 + "r"_4) + "r"_3"r"_4)/("r"_3 + "r"_4) Omega`
संबंधित प्रश्न
Complete the following :-
(a)

A piece of wire of resistance R is cut into five equal parts. These parts are then connected in parallel. If the equivalent resistance of this combination is R’, then the ratio `"R"/"R'"` is ______.
What possible values of resultant resistance one can get by combining two resistances, one of value 2 ohm and the other 6 ohm?
State and explain the laws of resistance.
Six resistances are connected together as shown in the figure. Calculate the equivalent resistance between points A and B.

What is the equivalent resistance between the points X and Y for the given network?
Six equal resistors of 1 ohm each are connected to form the sides of a hexagon ABCDEF. Calculate the resistance offered by the combination if the current enters at A and leaves it at D.
A metal wire of resistance 6 Ω is stretched so that its length is increased to twice its original length. Calculate its new resistance.
Show how you would connect three resistors, each of resistance 6 Ω, so that the combination has a resistance of 4 Ω.
