Advertisements
Advertisements
प्रश्न
चित्र (a) में k बल-स्थिरांक की किसी कमानी के एक सिरे को किसी दृढे आधार से जकड़ा तथा दूसरे मुक्त सिरे से एक द्रव्यमान m जुड़ा दर्शाया गया है। कमानी के मुक्त सिरे पर बल F आरोपित करने से कमानी तन जाती है चित्र (b) में उसी कमानी के दोनों मुक्त सिरों से द्रव्यमान जुड़ा दर्शाया गया है। कमानी के दोनों सिरों को चित्र में समान बल F द्वारा तानित किया गया है।
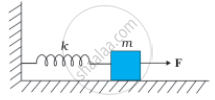
(a)
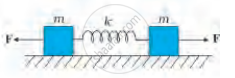
(b)
- दोनों प्रकरणों में कमानी का अधिकतम विस्तार क्या है?
- यदि (a) का द्रव्यमान तथा (b) के दोनों द्रव्यमानों को मुक्त छोड़ दिया जाए, तो प्रत्येक प्रकरण में दोलन का आवर्तकाल ज्ञात कीजिए।
उत्तर
- माना कमानी का अधिकतम विस्तार xmax है, तब
चित्र (a) में - F = kxmax
अधिकतम विस्तार `x_"max" = "F"/"k"`
(b) में-चूँकि इस बार कमानी किसी स्थिर वस्तु से संबद्ध नहीं है; अतः दूसरे पिण्ड पर लगे बल का कार्य केवल कमानी को स्थिर रखना है।
अतः विस्तार अभी भी केवल एक ही बल के कारण होगा।
∴ `"F" = "k""x"_"max"` से,
अधिकतम विस्थापन `x_"max" = "F"/"k"` - चित्र (a) में माना कि पिण्ड को खींचकर छोड़ने पर, वापसी की गति करता पिण्ड किसी क्षण साम्यावस्था से x दूरी पर है तब कमानी में प्रत्यानयन बल F = -kx होगा।
यदि पिण्ड का त्वरण ‘a है तो F = ma
∴ mα = -kx ⇒ `alpha = - ("k"/"m") x` ...(1)
स्पष्ट है की पिण्ड की गति सरल आवर्त गति है।
इस समीकरण से, `x/alpha = "m"/"k"`
∴ पिण्ड के दोलनों का आवर्तकाल `"T"= 2pisqrt(x/alpha)` या `"T" = 2pisqrt("m"/"k")`
चित्र (b) में-इस दशा में, निकाय का द्रव्यमान केन्द्र अर्थात् कमानी का मध्य बिन्दु स्थिर रहेगा और दोनों पिण्ड दोलन करेंगे।
इस अवस्था में हम मान सकते हैं कि प्रत्येक पिण्ड मूल कमानी की आधी लम्बाई से जुड़ा है तथा ऐसे प्रत्येक भाग का कमानी स्थिरांक 2k होगा। यदि किसी क्षण, कोई पिण्ड साम्यावस्था से x दूरी पर है तो कमानी के संगत भाग में प्रत्यानयन बल F = -2kx होगा। यदि पिण्ड का त्वरण a है तो
ma = F => ma = -2kx या ।
या `α = - ((2"k")/"m")x `
∴ पिण्ड की गति, सरल आवर्त गति है।
यहाँ `x/alpha = "m"/(2"k")`
∴ आवर्तकाल `"T" = 2pisqrt(x/alpha)` या `"T" = 2pi sqrt("m"/(2"k")`
APPEARS IN
संबंधित प्रश्न
अभ्यास प्रश्न 14.9 में, मान लीजिए जब कमानी अतानित अवस्था में है तब पिण्ड की स्थिति x = 0 है तथा बाएँ से दाएँ की दिशा x-अक्ष की धनात्मक दिशा है। दोलन करते पिण्ड के विस्थापन x को समय के फलन के रूप में दर्शाइए, जबकि विराम घड़ी को आरंभ (t = 0) करते समय पिण्ड
(a) अपनी माध्य स्थिति
(b) अधिकतम तानित स्थिति, तथा
(c) अधिकतम संपीडन की स्थिति पर है।
सरल आवर्त गति के लिए ये फलन एक-दूसरे से आवृत्ति में, आयाम में अथवा आरंभिक कला में किस रूप में भिन्न है ?
आधार क्षेत्रफल A तथा ऊँचाई h के एक कॉर्क का बेलनाकार टुकड़ा ρ1 घनत्व के किसी द्रव में तैर रहा है। कॉर्क को थोड़ा नीचे दबाकर स्वतंत्र छोड़ देते हैं, यह दर्शाइए कि कॉर्क ऊपर-नीचे सरल आवर्त दोलन करता है जिसका आवर्तकाल `"T"=2\pi \sqrt { \frac { "h"\rho }{ \rho _{ 1 }"g" } } ` है।
यहाँ ρ कॉर्क का घनत्व है (द्रव की श्यानता के कारण अवमंदन को नगण्य मानिए।)
आप किसी 3000 kg द्रव्यमान के स्वचालित वाहन पर सवार हैं। यह मानिए कि आप इस वाहन की निलंबन प्रणाली के दोलनी अभिलक्षणों का परीक्षण कर रहे हैं। जब समस्त वाहन इस पर रखा जाता है, तब निलंबन 15 cm आनमित होता है। साथ ही, एक पूर्ण दोलन की अवधि में दोलन के आयाम में 50% घटोतरी हो जाती है, निम्नलिखित के मान का आकलन कीजिए :
कमानी स्थिरांक
आप किसी 3000 kg द्रव्यमान के स्वचालित वाहन पर सवार हैं। यह मानिए कि आप इस वाहन की निलंबन प्रणाली के दोलनी अभिलक्षणों का परीक्षण कर रहे हैं। जब समस्त वाहन इस पर रखा जाता है, तब निलंबन 15 cm आनमित होता है। साथ ही, एक पूर्ण दोलन की अवधि में दोलन के आयाम में 50% घटोतरी हो जाती है, निम्नलिखित के मान का आकलन कीजिए :
कमानी तथा एक पहिए के प्रघात अवशोषक तंत्र के लिए अवमंदन स्थिरांक यह मानिए कि प्रत्येक पहिया 750 kg द्रव्यमान वहन करता है।
