Question

चित्र (a) में k बल-स्थिरांक की किसी कमानी के एक सिरे को किसी दृढे आधार से जकड़ा तथा दूसरे मुक्त सिरे से एक द्रव्यमान m जुड़ा दर्शाया गया है। कमानी के मुक्त सिरे पर बल F आरोपित करने से कमानी तन जाती है चित्र (b) में उसी कमानी के दोनों मुक्त सिरों से द्रव्यमान जुड़ा दर्शाया गया है। कमानी के दोनों सिरों को चित्र में समान बल F द्वारा तानित किया गया है।

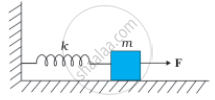
(a)

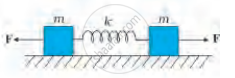
(b)

1. दोनों प्रकरणों में कमानी का अधिकतम विस्तार क्या है?
2. यदि (a) का द्रव्यमान तथा (b) के दोनों द्रव्यमानों को मुक्त छोड़ दिया जाए, तो प्रत्येक प्रकरण में दोलन का आवर्तकाल ज्ञात कीजिए।

Answer 1

1. माना कमानी का अधिकतम विस्तार x_max है, तब
   चित्र (a) में - F = kx_max
   अधिकतम विस्तार `x_"max" = "F"/"k"`
   (b) में-चूँकि इस बार कमानी किसी स्थिर वस्तु से संबद्ध नहीं है; अतः दूसरे पिण्ड पर लगे बल का कार्य केवल कमानी को स्थिर रखना है।
   अतः विस्तार अभी भी केवल एक ही बल के कारण होगा।
   ∴ `"F" = "k""x"_"max"` से,  
   अधिकतम विस्थापन `x_"max" = "F"/"k"`
2. चित्र (a) में माना कि पिण्ड को खींचकर छोड़ने पर, वापसी की गति करता पिण्ड किसी क्षण साम्यावस्था से x दूरी पर है तब कमानी में प्रत्यानयन बल F = -kx होगा।
   यदि पिण्ड का त्वरण ‘a है तो F = ma
   ∴ mα = -kx  ⇒ `alpha = - ("k"/"m") x`     ...(1)
   स्पष्ट है की पिण्ड की गति सरल आवर्त गति है।
   इस समीकरण से,  `x/alpha = "m"/"k"`
   ∴ पिण्ड के दोलनों का आवर्तकाल `"T"= 2pisqrt(x/alpha)`  या `"T" = 2pisqrt("m"/"k")`
   चित्र (b) में-इस दशा में, निकाय का द्रव्यमान केन्द्र अर्थात् कमानी का मध्य बिन्दु स्थिर रहेगा और दोनों पिण्ड दोलन करेंगे।
   इस अवस्था में हम मान सकते हैं कि प्रत्येक पिण्ड मूल कमानी की आधी लम्बाई से जुड़ा है तथा ऐसे प्रत्येक भाग का कमानी स्थिरांक 2k होगा। यदि किसी क्षण, कोई पिण्ड साम्यावस्था से x दूरी पर है तो कमानी के संगत भाग में प्रत्यानयन बल F = -2kx होगा। यदि पिण्ड का त्वरण a है तो
   ma = F => ma = -2kx या ।
   या `α = - ((2"k")/"m")x `
   ∴ पिण्ड की गति, सरल आवर्त गति है।
   यहाँ `x/alpha = "m"/(2"k")`
   ∴ आवर्तकाल `"T" = 2pisqrt(x/alpha)` या  `"T" = 2pi sqrt("m"/(2"k")`