Advertisements
Advertisements
प्रश्न
अभ्यास प्रश्न 14.9 में, मान लीजिए जब कमानी अतानित अवस्था में है तब पिण्ड की स्थिति x = 0 है तथा बाएँ से दाएँ की दिशा x-अक्ष की धनात्मक दिशा है। दोलन करते पिण्ड के विस्थापन x को समय के फलन के रूप में दर्शाइए, जबकि विराम घड़ी को आरंभ (t = 0) करते समय पिण्ड
(a) अपनी माध्य स्थिति
(b) अधिकतम तानित स्थिति, तथा
(c) अधिकतम संपीडन की स्थिति पर है।
सरल आवर्त गति के लिए ये फलन एक-दूसरे से आवृत्ति में, आयाम में अथवा आरंभिक कला में किस रूप में भिन्न है ?
उत्तर
उपर्युक्त प्रश्न में आयाम a = 0.20 m =2 cm।
कोणीय आवृत्ति `ω = sqrt("k"//"m")`
`= sqrt(1200//3)`
= 20 रे/से
(a) सरल आवर्त गति के समीकरण x = αsin (ωt + φ) ...(1)
यहाँ t = 0, x = 0
अतः समीकरण (1) से 0 = αsinφ ⇒ φ = 0
∴ समीकरण x = 2.0 sin 20t (सेमी में)
(b) t = 0 पर अधिकतम तानित स्थिति में x + α
समीकरण (1) से α = αsin(φ) ⇒ sin φ = 1 या φ = π/2
अतः समीकरण `x = alpha"sin"(ω"t" + pi/2)` या x = αcosωt
अर्थात x = 2.0 cos (20t) (सेमी में)
(c) t = 0 पर अधिकतम तानित स्थिति में x = - α
समीकरण (1) से, - α = α sinφ
⇒ sin φ = -1 या φ = 3π/2
अतः समीकरण x = α sin (ωt + 3π/2) = - α cos ωt
अर्थात x = - 2.0 cos 20t
APPEARS IN
संबंधित प्रश्न
चित्र (a) में k बल-स्थिरांक की किसी कमानी के एक सिरे को किसी दृढे आधार से जकड़ा तथा दूसरे मुक्त सिरे से एक द्रव्यमान m जुड़ा दर्शाया गया है। कमानी के मुक्त सिरे पर बल F आरोपित करने से कमानी तन जाती है चित्र (b) में उसी कमानी के दोनों मुक्त सिरों से द्रव्यमान जुड़ा दर्शाया गया है। कमानी के दोनों सिरों को चित्र में समान बल F द्वारा तानित किया गया है।
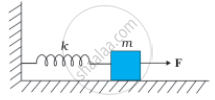
(a)
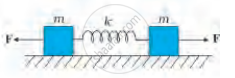
(b)
- दोनों प्रकरणों में कमानी का अधिकतम विस्तार क्या है?
- यदि (a) का द्रव्यमान तथा (b) के दोनों द्रव्यमानों को मुक्त छोड़ दिया जाए, तो प्रत्येक प्रकरण में दोलन का आवर्तकाल ज्ञात कीजिए।
आधार क्षेत्रफल A तथा ऊँचाई h के एक कॉर्क का बेलनाकार टुकड़ा ρ1 घनत्व के किसी द्रव में तैर रहा है। कॉर्क को थोड़ा नीचे दबाकर स्वतंत्र छोड़ देते हैं, यह दर्शाइए कि कॉर्क ऊपर-नीचे सरल आवर्त दोलन करता है जिसका आवर्तकाल `"T"=2\pi \sqrt { \frac { "h"\rho }{ \rho _{ 1 }"g" } } ` है।
यहाँ ρ कॉर्क का घनत्व है (द्रव की श्यानता के कारण अवमंदन को नगण्य मानिए।)
आप किसी 3000 kg द्रव्यमान के स्वचालित वाहन पर सवार हैं। यह मानिए कि आप इस वाहन की निलंबन प्रणाली के दोलनी अभिलक्षणों का परीक्षण कर रहे हैं। जब समस्त वाहन इस पर रखा जाता है, तब निलंबन 15 cm आनमित होता है। साथ ही, एक पूर्ण दोलन की अवधि में दोलन के आयाम में 50% घटोतरी हो जाती है, निम्नलिखित के मान का आकलन कीजिए :
कमानी स्थिरांक
आप किसी 3000 kg द्रव्यमान के स्वचालित वाहन पर सवार हैं। यह मानिए कि आप इस वाहन की निलंबन प्रणाली के दोलनी अभिलक्षणों का परीक्षण कर रहे हैं। जब समस्त वाहन इस पर रखा जाता है, तब निलंबन 15 cm आनमित होता है। साथ ही, एक पूर्ण दोलन की अवधि में दोलन के आयाम में 50% घटोतरी हो जाती है, निम्नलिखित के मान का आकलन कीजिए :
कमानी तथा एक पहिए के प्रघात अवशोषक तंत्र के लिए अवमंदन स्थिरांक यह मानिए कि प्रत्येक पहिया 750 kg द्रव्यमान वहन करता है।
