Advertisements
Advertisements
प्रश्न
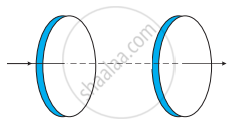
चित्र में एक संधारित्र दर्शाया गया है जो 12 cm त्रिज्या की दो वृत्ताकार प्लेटों को 5.0 cm की दूरी पर रखकर बनाया गया है। संधारित्र को एक बाह्य स्रोत (जो चित्र में नहीं दर्शाया गया है) द्वारा आवेशित किया जा रहा है। आवेशकारी धारा नियत है और इसका मान 0.15 A है।
- धारिता एवं प्लेटों के बीच विभवांतर परिवर्तन की दर का परिकलन कीजिए।
- प्लेटों के बीच विस्थापन धारा ज्ञात कीजिए।
- क्या किरचॉफ का प्रथम नियम संधारित्र की प्रत्येक प्लेट पर लागू होता है? स्पष्ट कीजिए।
उत्तर
प्रत्येक वृत्ताकार प्लेट की त्रिज्या r = 12 cm = 0.12 m
प्लेटों के बीच की दूरी d = 5 cm = 0.05 m
आवेशकारी धारा I = 0.15 A
चुंबकशीलता ε0 = 8.854 × 10−12 C2 N−1 m−2
(a) संधारित्र की धारिता C = `(epsilon_0"A")/"d"` ....[∵ A = πr2 = 3.14 × (0.12)2]
`= (8.854 xx 10^-12 xx 3.14 xx (0.12)^2)/0.05`
= 8.01 × 10−12 F
= 8.01 pF
किसी क्षण संधारित्र पर आवेश q = CV ⇒ V = `"q"/"C"`
`therefore "dV"/"dt" = 1/"C" "dq"/"dt" = 1/"C" "I" ...(because "dq"/"dt" = "I")`
∴ विभवांतर परिवर्तन की दर `"dV"/"dt" = 0.15/(8.01 xx 10^-12)`
= 1.875 × 109 V s−1
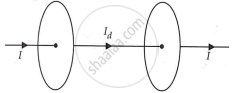
(b) प्लेटों पर विस्थापन धारा,
`"I"_"d" = epsilon_0 ("d"phi_"E")/"dt"`
जहाँ `phi_"E"` प्लेटों के बीच स्थित किसी बंद लूप से गुजरने वाला विद्युत फ्लक्स है।
∵ प्लेटों के बीच विद्युत क्षेत्र E = `"q"/(epsilon_0 "A")`
∴ यदि लूप का क्षेत्रफल A है तो,
`phi_"E" = oint vec("E") * "d" vec("A") = oint "E dA" ....[because vec("E") ⊥ "d" vec("A")]`
`=> phi_"E" = "EA" = "q"/epsilon_0 => ("d"phi_"E")/"dt" = 1/epsilon_0 * "dq"/"dt"`
∴ `"I"_"d" = epsilon_0 1/epsilon_0 "dq"/"dt" = "I"`
⇒ विस्थापन धारा, `"I"_"d"` = 0.15 A
(c) हाँ, किरचॉफ का प्रथम नियम संधारित्र की प्रत्येक प्लेट पर भी लागू होता है, क्योंकि Id = I होता है।
इसलिए प्रत्येक प्लेट में धारा निरंतर और स्थिर होती है।
APPEARS IN
संबंधित प्रश्न
एक समतल विद्युतचुंबकीय तरंग निर्वात में z-अक्ष के अनुदिश चल रही है। इसके विद्युत तथा चुंबकीय-क्षेत्रों के सदिश की दिशा के बारे में आप क्या कहेंगे? यदि तरंग की आवृत्ति 30 MHz हो तो उसकी तरंगदैर्घ्य कितनी होगी?
एक आवेशित कण अपनी माध्य साम्यावस्था के दोनों ओर 109 Hz आवृत्ति से दोलन करता है। दोलक द्वारा जनित विद्युतचुंबकीय तरंगों की आवृत्ति कितनी है?
निर्वात में एक आवर्त विद्युतचुंबकीय तरंग के चुंबकीय-क्षेत्र वाले भाग का आयाम B0 = 510 nT है। तरंग के विद्युत क्षेत्र वाले भाग का आयाम क्या है?
कल्पना कीजिए कि एक वैद्युतचुंबकीय तरंग के विद्युत क्षेत्र का आयाम E0 = 120 N/C है तथा इसकी आवृत्ति v = 50.0 MHz है।
- B0, ω, k तथा λ ज्ञात कीजिए।
- E तथा B के लिए व्यंजक प्राप्त कीजिए।
एक समतल em तरंग में विद्युत क्षेत्र, 2.0 × 1010 Hz आवृत्ति तथा 48 V m−1 आयाम से ज्यावक्रीय रूप से दोलन करता है।
- तरंग की तरंगदैर्घ्य कितनी है?
- दोलनशील चुंबकीय-क्षेत्र का आयाम क्या है?
- यह दर्शाइए E क्षेत्र का औसत ऊर्जा घनत्व, B क्षेत्र के औसत ऊर्जा घनत्व के बराबर है।
[c = 3 × 108 m s−1]
