Advertisements
Advertisements
प्रश्न
Choose the correct alternative:
A biconditional statement is the conjunction of two ______ statements
पर्याय
Negative
Compound
Connective
Conditional
उत्तर
Conditional
APPEARS IN
संबंधित प्रश्न
Examine whether each of the following statement patterns is a tautology or a contradiction or a contingency.
[~(~p ∧ ~q)] v q
Write down the following statements in symbolic form :
(A) A triangle is equilateral if and only if it is equiangular.
(B) Price increases and demand falls
Using truth table prove that ∼p ˄ q ≡ (p ˅ q) ˄ ∼p
Using the truth table, prove the following logical equivalence :
p ↔ q ≡ (p ∧ q) ∨ (~p ∧ ~q)
Write the following compound statement symbolically.
The angle is right angle if and only if it is of measure 90°.
Write the following compound statement symbolically.
If Δ ABC is right-angled at B, then m∠A + m∠C = 90°
Construct the truth table of the following statement pattern.
(p ∧ ∼q) ↔ (p → q)
Write the truth value of the following statement.
Earth is a planet and Moon is a star.
Write the negation of the following statement.
All men are animals.
Write the following statement in symbolic form.
Milk is white if and only if the sky is not blue.
Find the truth value of the following statement.
If a joint venture is a temporary partnership, then discount on purchase is credited to the supplier.
Find the truth value of the following statement.
3 is a prime number and an odd number.
If p and q are true and r and s are false, find the truth value of the following compound statement.
(p → q) ↔ ~(p ∨ q)
If p and q are true and r and s are false, find the truth value of the following compound statement.
~ [p ∨ (r ∧ s)] ∧ ~ [(r ∧ ~ s) ∧ q]
Assuming that the following statement is true,
p : Sunday is holiday,
q : Ram does not study on holiday,
find the truth values of the following statements.
If Sunday is not holiday then Ram studies on holiday.
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
p ↔ ~ q
Fill in the blanks :
Negation of “some men are animal” is –––––––––.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The Sun has set and Moon has risen.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The necessary condition for existence of a tangent to the curve of the function is continuity.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The drug is effective though it has side effects.
Assuming the first statement p and second as q. Write the following statement in symbolic form.
Even though it is not cloudy, it is still raining.
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
p → r
Rewrite the following statement without using conditional –
(Hint : p → q ≡ ∼ p ∨ q)
If demand falls, then price does not increase.
Assuming the following statement.
p : Stock prices are high.
q : Stocks are rising.
to be true, find the truth value of the following.
Stock prices are high or stocks are not rising iff stocks are rising.
Rewrite the following statement without using the connective ‘If ... then’.
If 10 − 3 = 7 then 10 × 3 ≠ 30.
Write the negation of the following statement.
I will have tea or coffee.
The negation of the statement (p ˄ q) `→` (r ˅ ∼ p) is ______.
Without using truth table show that -
(p ˅ q) ˄ (∼p v ∼q) ≡ (p ∧ ∼q) ˄ (∼p ∧ q)
Write the negation of p → q
Write the following statements in symbolic form.
If Qutub – Minar is in Delhi then Taj-Mahal is in Agra
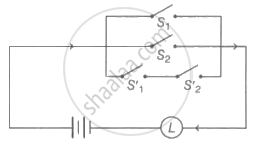
The symbolic form of the following circuit is (where p, q represents switches S1 and S2 closed respectively)
If c denotes the contradiction then the dual of the compound statement ∼p ∧ (q ∨ c) is ______
If p and q are true and rands are false statements, then which of the following is true?
The logical statement (∼p → q) ∧ (q → p) is equivalent to: ______
If p : A man is happy, q : A man is rich, then the symbolic form of ‘A man is neither happy nor rich is ______.
Write the following statement in symbolic form.
4 is an odd number if 3 is not a prime factor of 6.
Using truth table prove that:
~ (p `leftrightarrow` q) ≡ (p ∧ ~ q) ∨ (q ∧ ~ p)
