Advertisements
Advertisements
प्रश्न
Choose the correct alternative:
`lim_(x -> 0) ("e"^(sin x) - 1)/x` =
पर्याय
1
e
`1/"e"`
0
उत्तर
1
APPEARS IN
संबंधित प्रश्न
Evaluate the following limit:
`lim_(x -> 5)[(x^3 - 125)/(x^5 - 3125)]`
Evaluate the following limit:
If `lim_(x -> 1)[(x^4 - 1)/(x - 1)]` = `lim_(x -> "a")[(x^3 - "a"^3)/(x - "a")]`, find all possible values of a
Evaluate the following limit :
`lim_(y -> 1)[(2y - 2)/(root(3)(7 + y) - 2)]`
Evaluate the following limit :
`lim_(z -> "a")[((z + 2)^(3/2) - ("a" + 2)^(3/2))/(z - "a")]`
In the following example, given ∈ > 0, find a δ > 0 such that whenever, |x – a| < δ, we must have |f(x) – l| < ∈.
`lim_(x -> 2)(2x + 3)` = 7
In problems 1 – 6, using the table estimate the value of the limit
`lim_(x -> 0) (cos x - 1)/x`
| x | – 0.1 | – 0.01 | – 0.001 | 0.0001 | 0.01 | 0.1 |
| f(x) | 0.04995 | 0.0049999 | 0.0004999 | – 0.0004999 | – 0.004999 | – 0.04995 |
In exercise problems 7 – 15, use the graph to find the limits (if it exists). If the limit does not exist, explain why?
`lim_(x -> 1) f(x)` where `f(x) = {{:(x^2 + 2",", x ≠ 1),(1",", x = 1):}`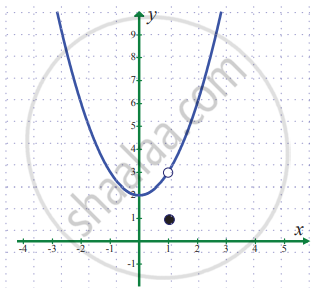
Sketch the graph of f, then identify the values of x0 for which `lim_(x -> x_0)` f(x) exists.
f(x) = `{{:(x^2",", x ≤ 2),(8 - 2x",", 2 < x < 4),(4",", x ≥ 4):}`
Sketch the graph of a function f that satisfies the given value:
f(– 2) = 0
f(2) = 0
`lim_(x -> 2) f(x)` = 0
`lim_(x -> 2) f(x)` does not exist.
Evaluate the following limits:
`lim_(sqrt(x) -> 3) (x^2 - 81)/(sqrt(x) - 3)`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(1 + x) - 1)/x`
Evaluate the following limits:
`lim_(x -> 0) (sqrt(1 - x) - 1)/x^2`
Evaluate the following limits:
`lim_(x -> oo) (1 + x - 3x^3)/(1 + x^2 +3x^3)`
Evaluate the following limits:
`lim_(x -> 0) (sin^3(x/2))/x^2`
Evaluate the following limits:
`lim_(alpha -> 0) (sin(alpha^"n"))/(sin alpha)^"m"`
Evaluate the following limits:
`lim_(x -> pi) (1 + sinx)^(2"cosec"x)`
Choose the correct alternative:
`lim_(theta -> 0) (sinsqrt(theta))/(sqrt(sin theta)`
Choose the correct alternative:
`lim_(x -> 0) (8^x - 4x - 2^x + 1^x)/x^2` =
Choose the correct alternative:
`lim_(x -> 0) ("e"^tanx - "e"^x)/(tan x - x)` =
Choose the correct alternative:
The value of `lim_(x -> 0) sinx/sqrt(x^2)` is
