Advertisements
Advertisements
प्रश्न
Choose the correct alternative:
If f(x) = x2 – 3x, then the points at which f(x) = f’(x) are
पर्याय
both positive integers
both negative integers
both irrational
one rational and another irrational
उत्तर
both irrational
APPEARS IN
संबंधित प्रश्न
Find the derivatives of the following functions using first principle.
f(x) = 6
Find the derivatives of the following functions using first principle.
f(x) = – 4x + 7
Find the derivatives of the following functions using first principle.
f(x) = – x2 + 2
Find the derivatives from the left and from the right at x = 1 (if they exist) of the following functions. Are the functions differentiable at x = 1?
`f(x) = |x - 1|`
Find the derivatives from the left and from the right at x = 1 (if they exist) of the following functions. Are the functions differentiable at x = 1?
`f(x) = sqrt(1 - x^2)`
Find the derivatives from the left and from the right at x = 1 (if they exist) of the following functions. Are the functions differentiable at x = 1?
`f(x) = {{:(x",", x ≤ 1),(x^2",", x > 1):}`
Determine whether the following function is differentiable at the indicated values.
f(x) = |x2 – 1| at x = 1
Determine whether the following function is differentiable at the indicated values.
f(x) = |x| + |x – 1| at x = 0, 1
Show that the following functions are not differentiable at the indicated value of x.
`f(x) = {{:(-x + 2, x ≤ 2),(2x - 4, x > 2):}` , x = 2
The graph of f is shown below. State with reasons that x values (the numbers), at which f is not differentiable.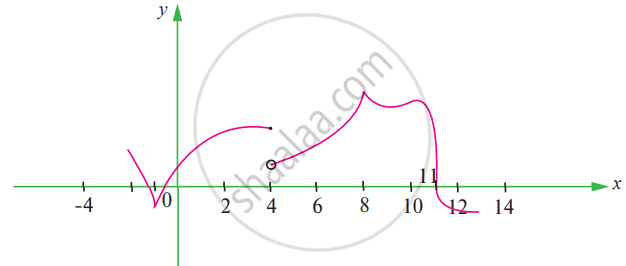
Examine the differentiability of functions in R by drawing the diagram
|cos x|
Choose the correct alternative:
f y = f(x2 + 2) and f'(3) = 5 , then `("d"y)/("d"x)` at x = 1 is
Choose the correct alternative:
If pv = 81, then `"dp"/"dv"` at v = 9 is
Choose the correct alternative:
It is given that f'(a) exists, then `lim_(x -> "a") (xf("a") - "a"f(x))/(x - "a")` is
Choose the correct alternative:
If f(x) = `{{:(x + 1, "when" x < 2),(2x - 1, "when" x ≥ 2):}` , then f'(2) is
Choose the correct alternative:
If g(x) = (x2 + 2x + 1) f(x) and f(0) = 5 and `lim_(x -> 0) (f(x) - 5)/x` = 4, then g'(0) is
