Advertisements
Advertisements
प्रश्न
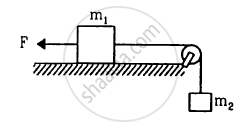
Consider the situation shown in figure. The force F is equal to the m2 g/2. If the area of cross section of the string is A and its Young modulus Y, find the strain developed in it. The string is light and there is no friction anywhere.
उत्तर
Given:
Force (F) = m2g/2
Area of cross-section of the string = A
Young's modulus = Y
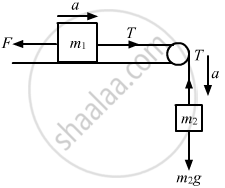
Let a be the acceleration produced in block m2 in the downward direction and T be the tension in the string.
From the free body diagram:
\[\text{m}_2 \text{g - T = m}_2 \text{a} . . . \left( \text{i} \right)\]
\[\text{ T - F = m}_1 \text{a . . . (ii)}\]
From equations (i) and (ii), we get:
\[a = \frac{\text{m}_2 \text{g - F}}{\text{m}_1 + \text{m}_2}\]
\[\text{ Applying F }= \frac{\text{m}_2 \text{g}}{2}\]
\[ \Rightarrow a = \frac{\text{m}_2 \text{g}}{2\left( \text{m}_1 + \text{m}_2 \right)}\]
Again, T = F + m1a
On applying the values of F and a, we get:
\[ \Rightarrow \text{ Strain }= \frac{∆ \text{L}}{\text{L}} = \frac{\text{F}}{\text{AY}}\]
\[ \Rightarrow \text{ Strain } = \frac{\left( \text{m}_2^2 + 2 \text{m}_1 \text{m}_2 \right)\text{g}}{2\left( \text{m}_1 + \text{m}_2 \right) \text{AY}}\]
\[ = \frac{\text{m}_2 g\left( 2 \text{m}_1 + \text{m}_2 \right)}{2\text{AY} \left( \text{m}_1 + \text{m}_2 \right)}\]
APPEARS IN
संबंधित प्रश्न
A steel wire of length 4.7 m and cross-sectional area 3.0 × 10–5 m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4.0 × 10–5 m2 under a given load. What is the ratio of Young’s modulus of steel to that of copper?
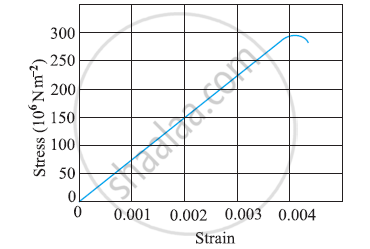
The figure shows the strain-stress curve for a given material. What are (a) Young’s modulus and (b) approximate yield strength for this material?
The stress-strain graphs for materials A and B are shown in Figure
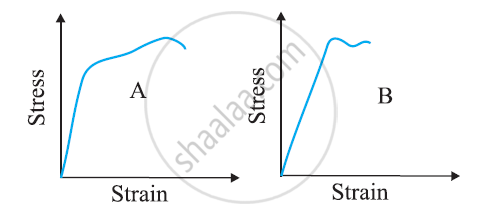
The graphs are drawn to the same scale.
(a) Which of the materials has the greater Young’s modulus?
(b) Which of the two is the stronger material?
A steel rod of cross-sectional area 4 cm2 and 2 m shrinks by 0.1 cm as the temperature decreases in night. If the rod is clamped at both ends during the day hours, find the tension developed in it during night hours. Young modulus of steel = 1.9 × 1011 N m−2.
A copper wire of cross-sectional area 0.01 cm2 is under a tension of 20N. Find the decrease in the cross-sectional area. Young modulus of copper = 1.1 × 1011 N m−2 and Poisson ratio = 0.32.
`["Hint" : (Delta"A")/"A"=2(Delta"r")/"r"]`
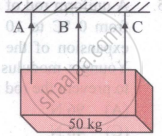
A uniform rectangular block of mass of 50 kg is hung horizontally with the help of three wires A, B and C each of length and area of 2m and 10mm2 respectively as shown in the figure. The central wire is passing through the centre of gravity and is made of material of Young's modulus 7.5 x 1010 Nm−2 and the other two wires A and C symmetrically placed on either side of the wire B are of Young's modulus 1011 Nm−2 The tension in the wires A and B will be in the ratio of:
The temperature of a wire is doubled. The Young’s modulus of elasticity ______.
A rigid bar of mass M is supported symmetrically by three wires each of length l. Those at each end are of copper and the middle one is of iron. The ratio of their diameters, if each is to have the same tension, is equal to ______.
The Young’s modulus for steel is much more than that for rubber. For the same longitudinal strain, which one will have greater tensile stress?
Identical springs of steel and copper are equally stretched. On which, more work will have to be done?
If the yield strength of steel is 2.5 × 108 Nm–2, what is the maximum weight that can be hung at the lower end of the wire?
A steel rod of length 2l, cross sectional area A and mass M is set rotating in a horizontal plane about an axis passing through the centre. If Y is the Young’s modulus for steel, find the extension in the length of the rod. (Assume the rod is uniform.)
In nature, the failure of structural members usually result from large torque because of twisting or bending rather than due to tensile or compressive strains. This process of structural breakdown is called buckling and in cases of tall cylindrical structures like trees, the torque is caused by its own weight bending the structure. Thus the vertical through the centre of gravity does not fall within the base. The elastic torque caused because of this bending about the central axis of the tree is given by `(Ypir^4)/(4R) . Y` is the Young’s modulus, r is the radius of the trunk and R is the radius of curvature of the bent surface along the height of the tree containing the centre of gravity (the neutral surface). Estimate the critical height of a tree for a given radius of the trunk.
If Y, K and η are the values of Young's modulus, bulk modulus and modulus of rigidity of any material respectively. Choose the correct relation for these parameters.
A boy's catapult is made of rubber cord which is 42 cm long, with a 6 mm diameter of cross-section and negligible mass. The boy keeps a stone weighing 0.02 kg on it and stretches the cord by 20 cm by applying a constant force. When released, the stone flies off with a velocity of 20 ms-1. Neglect the change in the area of the cross-section of the cord while stretched. Young's modulus of rubber is closest to ______.
A uniform metal rod of 2 mm2 cross section is heated from 0°C to 20°C. The coefficient of linear expansion of the rod is 12 × 10-6/°C, it's Young's modulus is 1011 N/m2. The energy stored per unit volume of the rod is ______.
If the length of a wire is made double and the radius is halved of its respective values. Then, Young's modules of the material of the wire will ______.
The force required to stretch a wire of cross section 1 cm2 to double its length will be ______.
(Given Young's modulus of the wire = 2 × 1011 N/m2)
