Advertisements
Advertisements
प्रश्न
Construct two concentric circles with centre O with radii 3 cm and 5 cm. Construct a tangent to a smaller circle from any point A on the larger circle. Measure and write the length of the tangent segment. Calculate the length of the tangent segment using Pythagoras' theorem.
उत्तर
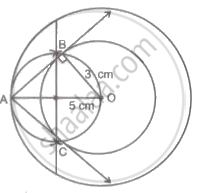
Step 1: At O, draw a circle with a radius of 3 cm.
Step 2: Draw a circle with a radius of 5 cm and a centre point of O. Join any point A on this circle to OA.
Step 3: P is the midpoint of OA, so divide it.
Step 4: Draw a circle with P as the centre and PO as the outside. Allow it to connect the smaller circle at B and C.
Step 5: Join AB and AC.
As a result, AB and AC are needed tangents.
From the figure, ΔAOB is a right-angle triangle.
∴ By Pythagoras' theorem,
AO2 = OB2 + AB2
∴ (5)2 = (3)2 + AB2
∴ 25 = 9 + AB2
∴ AB2 = 25 – 9
∴ AB2 = 16
∴ AB = 4
∴ The length of the tangent is 4 cm.
APPEARS IN
संबंधित प्रश्न
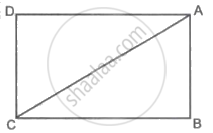
In the above figure `square`ABCD is a rectangle. If AB = 5, AC = 13, then complete the following activity to find BC.
Activity: ΔABC is a `square` triangle.
∴ By Pythagoras theorem
AB2 + BC2 = AC2
∴ 25 + BC2 = `square`
∴ BC2 = `square`
∴ BC = `square`
In the right-angled triangle ABC, Hypotenuse AC = 10 and side AB = 5, then what is the measure of ∠A?
If tan θ = `12/5`, then 5 sin θ – 12 cos θ = ?
From the information in the figure, complete the following activity to find the length of the hypotenuse AC.

AB = BC = `square`
∴ ∠BAC = `square`
Side opposite angle 45° = `square/square` × Hypotenuse
∴ `5sqrt(2) = 1/square` × AC
∴ AC = `5sqrt(2) xx square = square`
AB, BC and AC are three sides of a right-angled triangle having lengths 6 cm, 8 cm and 10 cm, respectively. To verify the Pythagoras theorem for this triangle, fill in the boxes:
ΔABC is a right-angled triangle and ∠ABC = 90°.
So, by the Pythagoras theorem,
`square` + `square` = `square`
Substituting 6 cm for AB and 8 cm for BC in L.H.S.
`square` + `square` = `square` + `square`
= `square` + `square`
= `square`
Substituting 10 cm for AC in R.H.S.
`square` = `square`
= `square`
Since, L.H.S. = R.H.S.
Hence, the Pythagoras theorem is verified.
There is a ladder of length 32 m which rests on a pole. If the height of pole is 18 m, determine the distance between the foot of ladder and the pole.
A person starts his trip from home. He moves 24 km in south direction and then starts moving towards east. He travels 7 km in that direction and finally reaches his destination. How far is the destination from his home?
Find the side of a square whose diagonal is `10sqrt2` cm.
