Advertisements
Advertisements
प्रश्न
D और E क्रमश : ∆ABC की भुजा AB और AC के मध्य-बिंदु हैं। DE को F तक बढ़ाया जाता है। यह सिद्ध करने के लिए कि CF रेखाखंड DA के बराबर और समांतर है। हमें एक अतिरिक्त सूचना की आवश्यकता है, जो है ______।
पर्याय
∠DAE = ∠EFC
AE = EF
DE = EF
∠ADE = ∠ECF
उत्तर
D और E क्रमश : ∆ABC की भुजा AB और AC के मध्य बिंदु हैं। DE को F तक बढ़ाया जाता है। यह सिद्ध करने के लिए कि CF रेखाखंड DA के बराबर और समांतर है। हमें एक अतिरिक्त सूचना की आवश्यकता है, जो है DE = EF।
स्पष्टीकरण -
हमने DE को F तक इस प्रकार बढ़ाया है कि
DE = EF ...(1)
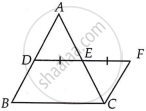
ΔADE और ΔCFE में,
AE = CE ...[चूँकि, E, AC का मध्य-बिंदु है।]
∠AED = ∠CEF ...[शीर्षाभिमुख कोण]
DE = FE ...[(1) द्वारा]
∴ ΔADE ≅ ΔCFE ...[SAS सर्वांगसमता द्वारा]
∴ AD = CF और ∠ADE = ∠CFE ...[C.P.C.T. द्वारा]
इससे पता चलता है कि एकांतर आंतरिक कोण बराबर होते हैं।
इस प्रकार, AD || CF
इसलिए, हमें जिस अतिरिक्त जानकारी की आवश्यकता है वह DE = EF है।
APPEARS IN
संबंधित प्रश्न
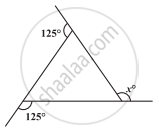
निम्नलिखित आकृति में x का मान ज्ञात कीजिए:
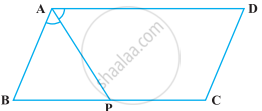
निम्नलिखित आकृति में, समांतर चतुर्भुज ABCD की भुजा BC पर एक बिंदु P इस प्रकार स्थित है। कि ∠BAP = ∠DAP है। सिद्ध कीजिए कि AD = 2CD है।
कोई वर्ग एक समद्विबाहु समकोण त्रिभुज के अंतर्गत इस प्रकार है कि वर्ग और त्रिभुज में एक कोण उभयनिष्ठ है। दर्शाइए कि वर्ग का शीर्ष जो उभयनिष्ठ कोण के शीर्ष के सम्मुख है कर्ण को समद्विभाजित करता है।
यदि किसी चतुर्भुज के तीन कोणों में से प्रत्येक कोण 75∘ के बराबर है, तो चौथा कोण है –
यदि एक चतुर्भुज के तीन कोणों में से प्रत्येक की माप 80∘ है, तब चौथे कोण की माप होगी –
निम्न में से कौन किसी चतुर्भुज के अंतःकोण हो सकते हैं?
किसी चतुर्भुज PQRS के कोण P, Q, R और S 1:3:7:9 के अनुपात में है। तब, PQRS है एक ______।
चतुर्भुज के सभी ______ का योग 360∘ है।
चतुर्भुज PQRS में, ∠P = 50∘, ∠Q = 50∘ और ∠R = 60∘ है। ∠S ज्ञात कीजिए। क्या यह चतुर्भुज उत्तल है या अवतल?
एक चतुर्भुज के तीन कोण बराबर हैं। चौथे कोण की माप 120∘ है। बराबर कोणों में से प्रत्येक की माप ज्ञात कीजिए।
