Advertisements
Advertisements
प्रश्न
Decide whether the following equation is quadratic equation or not.
\[x + \frac{1}{x} = - 2\]
उत्तर
\[x + \frac{1}{x} = - 2\]
Multiplying x by each term
`x xx x + x xx 1/x = x xx (-2)`
⇒x2 + 1 = -2x
x2 + 2x + 1 = 0
Only one variable x.
Maximum index = 2
So, it is a quadratic equation.
APPEARS IN
संबंधित प्रश्न
The divisor and quotient of the number 6123 are same and the remainder is half the divisor. Find the divisor.
The sum of the roots of the equation` x^2-6x+2=0`
(a) 2 (b)-2 (c)6 (d)-6
If one root of the equation` 3x^2-10x+3=0 is 1/3` then the other root is
(a) `-1/3` (b) `1/3` (c)`-3` (d)`3`
If the roots of the equation` ax^2+bx+c=0` are equal then c=?
(a)`b/(2a)` (b) `b/(2a)` (c) `-b^2/(4a)` (d) `B^2/(4a)`
Find the solution of the quadratic equation `3sqrt3x^2+10x+sqrt3=0`
If 1 is a root of the equation `ay^2+ay+3=0` and `y^2+y+b=0` then find the value of ab.
If the roots of the quadratic equation `px(x-2)+=0` are equal, find the value of p.
If 1 is a root of the equations ay2 + ay + 3 = 0 and y2 + y + b = 0 then ab equals: ?
Write the following equation in the form ax2 + bx + c= 0, then write the values of a, b, c for the equation.
3m2 = 2m2 – 9
Ranjana wants to distribute 540 oranges among some students. If 30 students were more each would get 3 oranges less. Find the number of students.
Solve the following quadratic equation.
m2 + 5m + 5 = 0
Find the value of m so that the quadratic equation mx (x − 7) + 49 = 0 has two equal roots.
If in an A. P., d = 10, find t6 - t2.
Find c if the system of equations cx+3y+(3 - c ) = 0, 12x + cy - c = 0 has infinitely many solutions?
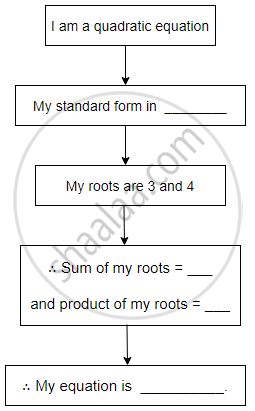
Complete the following activity to form a quadratic equation.
Activity:
Construct a word problem on quadratic equation, such that one of its answers is 20 (years, rupees, centimeter, etc.). Also, solve it.
In an orchard there are total 200 trees. If the number of trees in each column is more by 10 than the number of trees in each row, then find the number of trees in each row
Form a quadratic equation such that one of its roots is 5. Form a quadratic equation for it and write. (For the formation of word problems you can use quantities like age, rupees, or natural numbers.) (Sample solution for the above example is given below students can take another number to form another example)
Solution:
We need one of the solutions of the quadratic equation as 5.
Then we can take another root as any number like a positive or negative number or zero. Here I am taking another root of the quadratic equation as 2.
Then we can form a word problem as below,
Smita is younger than her sister Mita by 3 years (5 – 2 = 3). If the product of their ages is (5 × 2 = 10). Then find their present ages.
Let the age of Mita be x.
Therefore age of Smita = x – 3
By the given condition,
x(x – 3) = 10
x2 – 3x – 10 = 0
If 460 is divided by a natural number, then quotient is 2 more than nine times the divisor and remainder is 5. Find the quotient and divisor.
