Advertisements
Advertisements
प्रश्न
Define one tesla using the expression for the magnetic force acting on a particle of charge q moving with velocity \[\vec{v}\] in a magnetic field \[\vec{B}\] .
उत्तर
One tesla is the defined as the magnitude of magnetic field which produces a force of 1 newton when a charge of 1 coulomb moves perpendicularly in the region of the magnetic field at a velocity of 1 m/s.
\[F = \text{ qv } B\]
\[ \Rightarrow B = \frac{F}{\text{qv}}\]
\[ \Rightarrow 1 T = \frac{1 N}{\left( 1 C \right)\left( 1 \text{ m/s} \right)}\]
APPEARS IN
संबंधित प्रश्न
A rod of length l is moved horizontally with a uniform velocity 'v' in a direction perpendicular to its length through a region in which a uniform magnetic field is acting vertically downward. Derive the expression for the emf induced across the ends of the rod.
A horizontal overhead power line carries a current of 90 A in east to west direction. What is the magnitude and direction of the magnetic field due to the current 1.5 m below the line?
Magnetic lines of force always cross each other
Define magnetic lines of force
A steady current (I1) flows through a long straight wire. Another wire carrying steady current (I2) in the same direction is kept close and parallel to the first wire. Show with the help of a diagram how the magnetic field due to the current I1 exerts a magnetic force on the second wire. Write the expression for this force.
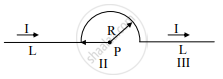
A conductor has three segments; two straights of length L and a semicircular with radius R. It carries a current I What is the magnetic field B at point P?
Explain "Magnetic force never does any work on moving charges".
A charged particle enters an environment of a strong and non-uniform magnetic field varying from point to point both in magnitude and direction, and comes out of it following a complicated trajectory. Would its final speed equal the initial speed if it suffered no collisions with the environment?
Two charged particles traverse identical helical paths in a completely opposite sense in a uniform magnetic field B = B0k̂.
Write the expression for the Lorentz force on a particle of charge q moving with a velocity `vecv` in a magnetic field `vecB`. When is the magnitude of this force maximum? Show that no work is done by this force on the particle during its motion from point `vecr_1` to point `vecr_2`.
