Advertisements
Advertisements
प्रश्न
Define the e.m.f. (E) of a cell and the potential difference (V) of a resistor R in terms of the work done in moving a unit charge. State the relation between these two works and the work done in moving a unit charge through a cell connected across the resistor. Take the internal resistance of the cell as ‘r’. Hence obtain an expression for the current i in the circuit.
उत्तर
E. M. F. of a cell is generally defined as the amount of work done (or the energy spent) in taking a unit positive charge around the complete circuit of the cell (i.e., in the wire outside the cell and the electrolyte within the cell). It is also defined as the potential difference between the terminals of a cell when no current is drawn from it (or when the cell is in open circuit).
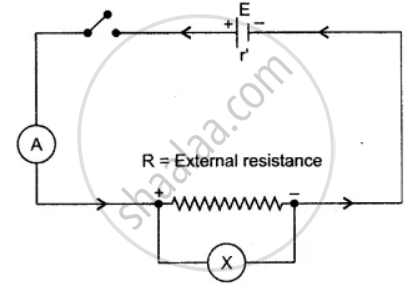
Potential difference (p.d.) or the terminal voltage of a cell is generally defined as the amount of work done in carrying a unit positive charge round the circuit connected across the terminals of the cell. If W is the amount of work done (in J) in moving a test charge q between the terminals of a cell through a resistor R, then the p.d. i.e., work done in moving a unit positive charge across the terminals of the cell.
Relation between E, V (p.d.), external resistance R and the internal resistance r’,
Applying Ohm's law to external resistance only
I = `"V"/"R"` .....(i)
Again applying Ohm's law to complete circuit
I = `"E"/("R" + "r")` ....(ii)
Comparing I in (i) and (ii), We have
`"V"/"R" = "E"/("R" + "r")`
APPEARS IN
संबंधित प्रश्न
A cell of Emf 2 V and internal resistance 1.2 Ω is connected with an ammeter of resistance 0.8 Ω and two resistors of 4.5 Ω and 9 Ω as shown in the diagram below:
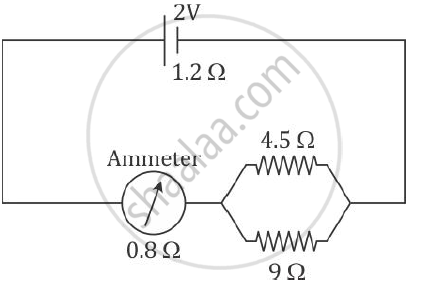
1) What would be the reading on the Ammeter?
2) What is the potential difference across the terminals of the cell?
Explain why the p.d across the terminals of a cell is more in an open circuit and reduced in a closed circuit.
A cell of e.m.f. 1.8V and internal resistance 2Ω is connected in series with an ammeter of resistance 0.7Ω and a resistor of 4.5Ω as shown in Fig.
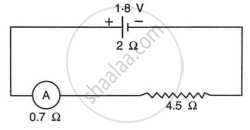
- What would be the reading of the ammeter?
- What is the potential difference across the terminals of the cell?
A cell of e.m.f. ε and internal resistance 𝔯 sends current 1.0 A when it is connected to an external resistance 1.9 Ω. But it sends current 0.5 A when it is connected to an external resistance 3.9 Ω. Calculate the values of ε and 𝔯.
What is the colour code for the insulation on the earth wire?
A cell of emf. 1.5 V and internal resistance 10 ohms is connected to a resistor of 5 ohms, with an ammeter in series see fig.. What is the reading of the ammeter?
A cell supplies a current of 0.6 A through a 2Ω coil and a current of 0.3 A through on 8Ω coil. Calculate the e.m.f and internal resistance of the cell.
(a) Calculate the total resistance across AB.
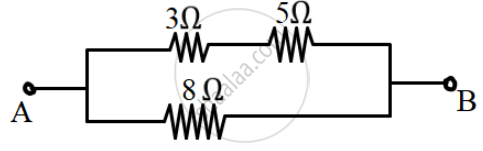
(b) If a cell of e.m.f 2.4 V with negligible internal resistance is connected across AB then calculate the current drawn from the cell.
Study the diagram:
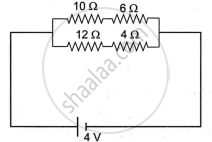
- Calculate the total resistance of the circuit.
- Calculate the current drawn from the cell.
- State whether the current through 10 Ω resistor is greater than, less than or equal to the current through the 12 Ω resistor.
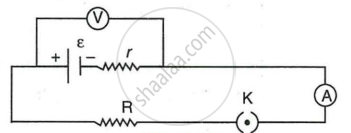
The diagram in Figure shows a cell of e.m.f. ε = 4 volt and internal resistance r = 2 ohm connected to an external resistance R = 8 ohm. The ammeter A measures the current in the circuit and the voltmeter V measures the terminal voltage across the cell. What will be the readings of the ammeter and voltmeter when
- the key K is open, and
- the key K is closed