Advertisements
Advertisements
प्रश्न
Derive an expression for the electric potential due to an electric dipole.
उत्तर
- Consider an electric dipole. Let origin be at the centre of the dipole as shown in the figure below.
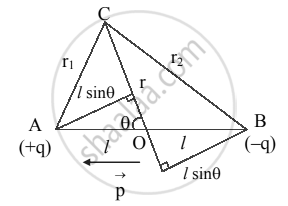
Electric potential due to an electric Dipole - Let C be any point near the electric dipole at a distance r from the centre O inclined at an angle θ with the axis of the dipole.
Let r1 and r2 be the distances of point C from charges +q and –q, respectively. - Potential at C due to charge +q at A is,
V1 = `(+"q")/(4piε_0"r"_1)`
Potential at C due to charge –q at B is,
V2 = `(-"q")/(4piε_0"r"_2)` - The potential at C due to the dipole is,
`"V"_"C" = "V"_1 + "V"_2 = "q"/(4piε_0)[1/"r"_1 - 1/"r"_2]` ….(1) - By geometry,
`"r"_1^2 = "r"^2 + "l"^2 - 2"rl" "cos"θ`
`"r"_2^2 = "r"^2 + "l"^2 + 2"rl" "cos"θ`
`"r"_1^2 = "r"^2(1 + "l"^2/"r"^2 - 2"l"/"r" cosθ)`
`"r"_2^2 = "r"^2(1 + "l"^2/"r"^2 + 2"l"/"r" cosθ)`
For a short dipole, 2l << r and
If r >> l; `"l"/"r"` is small
∴ `"l"^2/"r"^2` can be neglected
∴ `"r"_1^2 = "r"^2(1 - 2"l"/"r" cosθ)`
`"r"_2^2 = "r"^2(1 + (2"l")/"r" cosθ)`
∴ `"r"_1 = "r"(1 - (2l)/"r" cosθ)^{1/2}`
∴ `"r"_2 = "r"(1 + (2l)/"r" cosθ)^{1/2}`
∴ `1/"r"_1 = 1/"r"(1 - (2l)/"r"cosθ)^{(-1)/2}` and
`1/"r"_2 = 1/"r"(1 + (2l)/"r"cosθ)^{(-1)/2}` ….(2) - Using equations (1) and (2),
VC = V1 + V2
= `"q"/(4piepsilon_0)[1/"r"(1 - (2lcosθ)/"r")^{(-1)/2} - 1/"r"(1 + (2lcosθ)/"r")^{(-1)/2}]` - Using binomial expansion,
(1 + x)n = 1 + nx, x << l and retaining terms up to the first order of `l/"r"` only, we get
VC = `"q"/(4piepsilon_0) 1/"r" [(1 + l/"r" cosθ) - (1 - l/"r" cosθ)]`
= `"q"/(4piepsilon_0"r") [1 + l/"r" cosθ - 1 + l/"r" cosθ]`
= `"q"/(4piepsilon_0"r")["2l"/"r" cosθ]`
∴ `"V"_"C" = 1/(4piepsilon_0) ("p"cosθ)/"r"^2` ......(∵ p = q × 2l) - Electric potential at C, can also be expressed as,
`"V"_"C" = 1/(4piepsilon_0) (vec"p".vec"r")/("r"^3)`
`"V"_"C" = 1/(4piepsilon_0)(vec"p".hat"r")/("r"^2)`, `(hat"r" = vec"r"/"r")` .........`(hat"r" = vec"r"/"r")`
where `hat"r"` is a unit vector along the position vector `vec("OC") = hat"r"`
APPEARS IN
संबंधित प्रश्न
One hundred and twenty five small liquid drops, each carrying a charge of 0.5 µC and of diameter 0.1 m form a bigger drop. Calculate the potential at the surface of the bigger drop.
If an electron is brought towards another electron, the electric potential energy of the system ______.
Which physical quantity has its unit as J/C? Is it a scalar or vector?
Find the electric potential at the surface of an atomic nucleus (Z = 50) of radius 9 × 10-13 cm.
Three-point charges +q, +2q and Q are placed at the three vertices of an equilateral triangle. Find the value of charge Q (in terms of q), so that the electric potential energy of the system is zero.
Obtain an expression for the potential energy of a dipole in an external field.
An AC circuit contains resistance of 12Q and inductive reactance 5Q. The phase angle between current and potential difference will be ______.
In a certain region of space with volume 0.2 m3 , the electric potential is found to be 5V throughout. The magnitude of electric field in this region is: ____________.
The electric potential V at any point O (x, y, z all in metres) in space is given by V = 4x2 volt. The electric field at the point (1 m, 0, 2m) in volt/metre is ____________.
The potential differences that must be applied across the parallel and series combination of 3 identical capacitors are such that the energy stored in them becomes the same. The ratio of potential difference in parallel to series combination is ______
A capacitor C1 = 4µF is connected is series with another capacitor C2 = 1µF. The combination is connected across d.c. source of 200 V. The ratio of potential across C2 to that across C1 is ______.
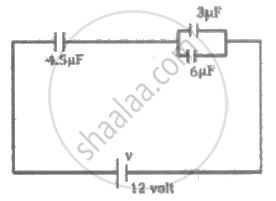
In the circuit shown, the potential difference across the 4.5 µF capacitor is ______.
Potential energy as a function of r is given by U = `"A"/"r"^10-"B"/"r"^5`, where r is the interatomic distance, A and B are positive constants. The equilibrium distance between the two atoms will be ______.
State the formula giving the relation between electric field intensity and potential gradient.
1 Weber/second is equal to ______.
Derive an expression for the electric potential energy of an electric dipole in a uniform electric field.
Derive the relation between electric intensity and electric potential.
