Advertisements
Advertisements
Question
Derive an expression for the electric potential due to an electric dipole.
Solution
- Consider an electric dipole. Let origin be at the centre of the dipole as shown in the figure below.
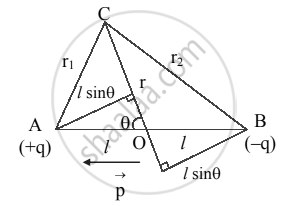
Electric potential due to an electric Dipole - Let C be any point near the electric dipole at a distance r from the centre O inclined at an angle θ with the axis of the dipole.
Let r1 and r2 be the distances of point C from charges +q and –q, respectively. - Potential at C due to charge +q at A is,
V1 = `(+"q")/(4piε_0"r"_1)`
Potential at C due to charge –q at B is,
V2 = `(-"q")/(4piε_0"r"_2)` - The potential at C due to the dipole is,
`"V"_"C" = "V"_1 + "V"_2 = "q"/(4piε_0)[1/"r"_1 - 1/"r"_2]` ….(1) - By geometry,
`"r"_1^2 = "r"^2 + "l"^2 - 2"rl" "cos"θ`
`"r"_2^2 = "r"^2 + "l"^2 + 2"rl" "cos"θ`
`"r"_1^2 = "r"^2(1 + "l"^2/"r"^2 - 2"l"/"r" cosθ)`
`"r"_2^2 = "r"^2(1 + "l"^2/"r"^2 + 2"l"/"r" cosθ)`
For a short dipole, 2l << r and
If r >> l; `"l"/"r"` is small
∴ `"l"^2/"r"^2` can be neglected
∴ `"r"_1^2 = "r"^2(1 - 2"l"/"r" cosθ)`
`"r"_2^2 = "r"^2(1 + (2"l")/"r" cosθ)`
∴ `"r"_1 = "r"(1 - (2l)/"r" cosθ)^{1/2}`
∴ `"r"_2 = "r"(1 + (2l)/"r" cosθ)^{1/2}`
∴ `1/"r"_1 = 1/"r"(1 - (2l)/"r"cosθ)^{(-1)/2}` and
`1/"r"_2 = 1/"r"(1 + (2l)/"r"cosθ)^{(-1)/2}` ….(2) - Using equations (1) and (2),
VC = V1 + V2
= `"q"/(4piepsilon_0)[1/"r"(1 - (2lcosθ)/"r")^{(-1)/2} - 1/"r"(1 + (2lcosθ)/"r")^{(-1)/2}]` - Using binomial expansion,
(1 + x)n = 1 + nx, x << l and retaining terms up to the first order of `l/"r"` only, we get
VC = `"q"/(4piepsilon_0) 1/"r" [(1 + l/"r" cosθ) - (1 - l/"r" cosθ)]`
= `"q"/(4piepsilon_0"r") [1 + l/"r" cosθ - 1 + l/"r" cosθ]`
= `"q"/(4piepsilon_0"r")["2l"/"r" cosθ]`
∴ `"V"_"C" = 1/(4piepsilon_0) ("p"cosθ)/"r"^2` ......(∵ p = q × 2l) - Electric potential at C, can also be expressed as,
`"V"_"C" = 1/(4piepsilon_0) (vec"p".vec"r")/("r"^3)`
`"V"_"C" = 1/(4piepsilon_0)(vec"p".hat"r")/("r"^2)`, `(hat"r" = vec"r"/"r")` .........`(hat"r" = vec"r"/"r")`
where `hat"r"` is a unit vector along the position vector `vec("OC") = hat"r"`
APPEARS IN
RELATED QUESTIONS
A charge 6 µC is placed at the origin and another charge - 5 µC is placed on the y-axis at A = (0, 6.0 m).

(a) Calculate the net electric potential at P = (8.0 m, 0).
(b) Calculate the work done in bringing a proton from infinity to point P. What is the significance of the negative sign?
One hundred and twenty five small liquid drops, each carrying a charge of 0.5 µC and of diameter 0.1 m form a bigger drop. Calculate the potential at the surface of the bigger drop.
If an electron is brought towards another electron, the electric potential energy of the system ______.
Which physical quantity has its unit as J/C? Is it a scalar or vector?
Three-point charges +q, +2q and Q are placed at the three vertices of an equilateral triangle. Find the value of charge Q (in terms of q), so that the electric potential energy of the system is zero.
Obtain an expression for the potential energy of a dipole in an external field.
An AC circuit contains resistance of 12Q and inductive reactance 5Q. The phase angle between current and potential difference will be ______.
In a certain region of space with volume 0.2 m3 , the electric potential is found to be 5V throughout. The magnitude of electric field in this region is: ____________.
Two parallel plates separated by a distance 'd' are kept at potential difference 'V' volt. A charge 'q' of mass 'm' enters in parallel plates with some velocity. The acceleration of the charged particle will be ______
The potential differences that must be applied across the parallel and series combination of 3 identical capacitors are such that the energy stored in them becomes the same. The ratio of potential difference in parallel to series combination is ______
A capacitor C1 = 4µF is connected is series with another capacitor C2 = 1µF. The combination is connected across d.c. source of 200 V. The ratio of potential across C2 to that across C1 is ______.
Potential energy as a function of r is given by U = `"A"/"r"^10-"B"/"r"^5`, where r is the interatomic distance, A and B are positive constants. The equilibrium distance between the two atoms will be ______.
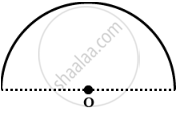
A semicircular wire of radius a having λ as charge per unit length is shown in the figure. Find the electric potential at the centre of the semicircular wire.
State the formula giving the relation between electric field intensity and potential gradient.
1 Weber/second is equal to ______.
Derive an expression for the electric potential energy of an electric dipole in a uniform electric field.
Derive the relation between electric intensity and electric potential.
