Advertisements
Advertisements
प्रश्न
Derive the expression for the self-inductance of a long solenoid of cross sectional area A and length l, having n turns per unit length.
Obtain an expression for self-inductance of a long solenoid of length l, area of cross-section A having N turns.
उत्तर
The self-inductance of a solenoid is defined as the magnetic flux to current ratio via the solenoid. It is given by,
L = `phi/I`
Total number of turns in the solenoid,
N = nl
The magnetic field inside the long solenoid,
B = μ0ni
Flux through one turn,
`phi_1 = BA = mu_0niA`
Thus, total flux through N turns,
`phi_t = Nphi_1 = nl xx mu_0niA = mu_0n^2lAi`
Using `phi_t = Li`
where L is the self-inductance of the coil.
∴ `mu_0n^2lAi = Li`
L = `mu_0n^2Al`
APPEARS IN
संबंधित प्रश्न
In a given coil of self-inductance of 5 mH, current changes from 4 A to 1 A in 30 ms. Calculate the emf induced in the coil.
An inductor of inductance 5.0 H, having a negligible resistance, is connected in series with a 100 Ω resistor and a battery of emf 2.0 V. Find the potential difference across the resistor 20 ms after the circuit is switched on.
Define self-inductance.
Obtain an expression for the self-inductance of a solenoid.
An e.m.f. of 10 volt is produced by a self inductance when the current changes at a steady rate from 6 A to 4 A in 1 millisecond. The value of self inductance is ____________.
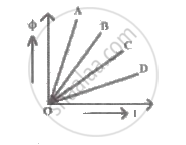
A graph of magnetic flux `phi` versus current (I) is shown for four inductors A, B, C, D. Smaller value of self inductance is for inductor ____________.
When current i passes through an inductor of self-inductance L, energy stored in it is 1/2. L i2. This is stored in the ______.
The self inductance L of a solenoid of length l and area of cross-section A, with a fixed number of turns N increases as ______.
Consider an infinitely long wire carrying a current I(t), with `(dI)/(dt) = λ` = constant. Find the current produced in the rectangular loop of wire ABCD if its resistance is R (Figure).

