Advertisements
Advertisements
प्रश्न
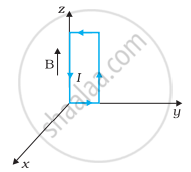
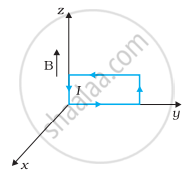
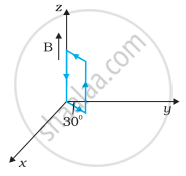
धनात्मक z-दिशा में 3000 G की एक एकसमान चुम्बकीय क्षेत्र लगाया गया है। एक आयताकार लूप जिसकी भुजाएँ 10 cm एवं 5 cm और जिसमें 12 A धारा प्रवाहित हो रही है, इस क्षेत्र में रखा है। चित्र 4.7 में दिखायी गई लूप की विभिन्न स्थितियों में इस पर लगने वाला बल-युग्म आघूर्ण क्या है? हर स्थिति में बल क्या है? स्थायी सन्तुलन वाली स्थिति कौन-सी है?
 |
 |
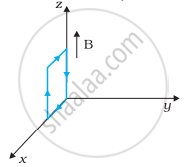 |
| (a) | (b) | (c) |
 |
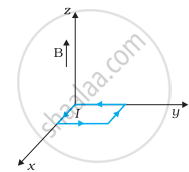 |
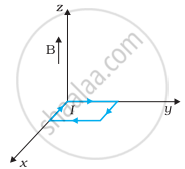 |
| (d) | (e) | (f) |
उत्तर
दिया है, B = 3000 G = 0.3 T, a = 0.1 m, b = 0.05 m, i = 12 A
कुंडली का क्षेत्रफल A = ab = 0.1 m x 0.05 m = 5 x 10-3 m
(a), (b), (c), (d) प्रत्येक दशा में कुंडली के तल पर अभिलम्ब, चुम्बकीय क्षेत्र के लम्बवत् है; अतः प्रत्येक दशा में
बल-युग्म का आघूर्ण τ = iAB sin 90° = 12 x 5 x 10-3 x 0.3 = 1.8 x 10-2 N-m
प्रत्येक दशा में बल शून्य है, क्योंकि एकसमान चुम्बकीय क्षेत्र में रखे धारालूप पर बल-युग्म कार्य करता है परन्तु बल नहीं।
(a) τ = 1.8 x 10-2 N-m ऋण y-अक्ष की दिशा में तथा बल शून्य है।
(b) τ = 1.8 x 10-2 N-m ऋण y-अक्ष की दिशा में तथा बल शून्य है।
(c) τ = 1.8 x 10-2 N-m ऋण x-अक्ष की दिशा में तथा बल शून्य है।
(d) τ = 1.8 x 10-2 N-m तथा बल शून्य है।
(e) तथा (f) दोनों स्थितियों में कुंडली के तल पर अभिलम्ब चुम्बकीय क्षेत्र के अनुदिश है; अत:
t = iAB sin 0° = 0
अत: इन दोनों दशाओं में बल-आघूर्ण व बल दोनों शून्य हैं। यह स्थितियाँ सन्तुलन की स्थायी अवस्था में दर्शाती हैं।
