Advertisements
Advertisements
प्रश्न
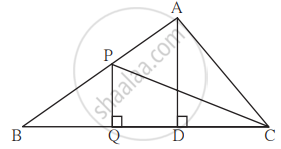
दिलेल्या आकृतीत, PQ ⊥ BC, AD ⊥ BC तर खालील गुणोत्तरे लिहा.
i) `"A(ΔPQB)"/"A(ΔPBC)"`
ii) `"A(ΔPBC)"/"A(ΔABC)"`
iii) `"A(ΔABC)"/"A(ΔADC)"`
iv) `"A(ΔADC)"/"A(ΔPQC)"`
उत्तर
i. ΔPQB आणि ΔPBC ची PQ ही सामाईक उंची आहे.
`"A(ΔPQB)"/"A(ΔPBC)" = "BQ"/"BC"` ........[समान उंचीचे त्रिकोण]
ii. ΔPBC आणि ΔABC चा BC हा सामाईक पाया आहे.
`"A(ΔPBC)"/"A(ΔABC)" = "PQ"/"AD"` .......[समान पाया असलेले त्रिकोण]
iii. ΔABC आणि ΔADC चा AD हा सामाईक पाया आहे.
`"A(ΔABC)"/"A(ΔADC)" = "BC"/"DC"` .......[समान उंचीचे त्रिकोण]
iv. `"A(ΔADC)"/"A(ΔPQC)" = ("DC" xx "AD")/("QC" xx "PQ")` .........[दोन त्रिकोणांच्या क्षेत्रफळांचे गुणोत्तर हे त्यांच्या पाया व संगत उंची यांच्या गुणाकारांच्या गुणोत्तराएवढे असते.]
APPEARS IN
संबंधित प्रश्न
एका त्रिकोणाचा पाया 9 आणि उंची 5 आहे. दुसऱ्या त्रिकोणाचा पाया 10 आणि उंची 6 आहे, तर त्या त्रिकोणांच्या क्षेत्रफळांचे गुणोत्तर काढा.
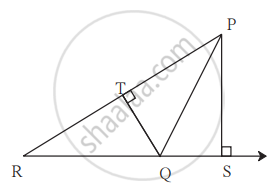
दिलेल्या आकृती मध्ये रेख PS ⊥ रेख RQ रेख QT ⊥ रेख PR. जर RQ = 6, PS = 6, PR = 12 तर QT काढा.
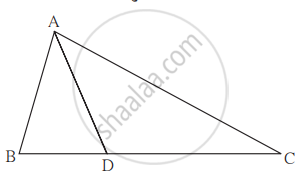
ΔABC मध्ये B - D – C आणि BD = 7, BC = 20 तर खालील गुणोत्तरे काढा.
- `("A"(Δ"ABD"))/("A"(Δ"ADC"))`
- `("A"(Δ"ABD"))/("A"(Δ"ABC"))`
- `("A"(Δ"ADC"))/("A"(Δ"ABC"))`
समान उंचीच्या दोन त्रिकोणांच्या क्षेत्रफळांचे गुणोत्तर 2 : 3 आहे, लहान त्रिकोणाचा पाया 6 सेमी असेल तर मोठ्या त्रिकोणाचा संगत पाया किती असेल?
जर ∆XYZ ~ ∆PQR, तर `"XY"/"PQ" = "YZ"/"QR"` = ?
दोन समरूप त्रिकोणांच्या क्षेत्रफळांचे गुणोत्तर 144:49 असेल, तर त्या त्रिकोणांच्या संगत बाजूंचे गुणोत्तर किती?
∆PQR ~ ∆SUV, तर त्या त्रिकोणाच्या एकरूप कोनांच्या जोड्या लिहा.
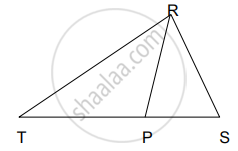
आकृतीमध्ये TP = 10 सेमी, PS = 6 सेमी. `("A"(Delta"RTP"))/("A"(Delta"RPS"))` = ?
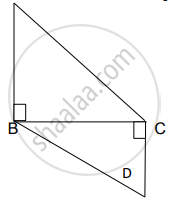
आकृतीमध्ये, AB लंब BC आणि DC लंब BC, AB = 6, DC = 4, तर `("A"(Delta"ABC"))/("A"(Delta"BCD"))` = ?
वास्तू विशारदाकडे इमारतीची प्रतिकृती आहे. प्रत्यक्ष इमारतीची लांबी 1 मीटर असल्यास प्रतिकृतीची लांबी 0.75 सेमी असेल, तर 22.5 मीटर लांबी आणि 10 मीटर उंची असलेल्या इमारतीच्या प्रतिकृतीची लांबी व उंची काढा.
