Advertisements
Advertisements
प्रश्न
Distance of the point (α, β, γ) from y-axis is ____________.
पर्याय
β
|β|
|b| + |γ|
`sqrt("a"^2 + γ^2)`
उत्तर
Distance of the point (α, β, γ) from y-axis is `sqrt("a"^2 + γ^2)`.
Explanation:
The given point is (α, β, γ)
Any point on y-axis = (0, β, 0)
∴ Required distance = `sqrt((alpha - 0)^2 + (beta - beta)^2 + (γ - 0)^2)`
= `sqrt(alpha^2 + γ^2)`
APPEARS IN
संबंधित प्रश्न
Find the equation of the planes parallel to the plane x + 2y+ 2z + 8 =0 which are at the distance of 2 units from the point (1,1, 2)
Find the distance of a point (2, 5, −3) from the plane `vec r.(6hati-3hatj+2 hatk)=4`
In the given cases, find the distance of each of the given points from the corresponding given plane
Point Plane
(3, – 2, 1) 2x – y + 2z + 3 = 0
In the given cases, find the distance of each of the given points from the corresponding given plane.
Point Plane
(2, 3, – 5) x + 2y – 2z = 9
Find the distance of the point (1, 2, –1) from the plane x - 2y + 4z - 10 = 0 .
Write the equation of a plane which is at a distance of \[5\sqrt{3}\] units from origin and the normal to which is equally inclined to coordinate axes.
Find the distance of the point \[2 \hat{i} - \hat{j} - 4 \hat{k}\] from the plane \[\vec{r} \cdot \left( 3 \hat{i} - 4 \hat{j} + 12 \hat{k} \right) - 9 = 0 .\]
Find the distance of the point (2, 3, −5) from the plane x + 2y − 2z − 9 = 0.
Find the equations of the planes parallel to the plane x + 2y − 2z + 8 = 0 that are at a distance of 2 units from the point (2, 1, 1).
Find the distance of the point (2, 3, 5) from the xy - plane.
Find the distance of the point (3, 3, 3) from the plane \[\vec{r} \cdot \left( 5 \hat{i} + 2 \hat{j} - 7k \right) + 9 = 0\]
Find the distance of the point (1, −2, 3) from the plane x − y + z = 5 measured parallel to the line whose direction cosines are proportional to 2, 3, −6.
If the product of the distances of the point (1, 1, 1) from the origin and the plane x − y + z+ λ = 0 be 5, find the value of λ.
Find the distance between the point (7, 2, 4) and the plane determined by the points A(2, 5, −3), B(−2, −3, 5) and C (5, 3, −3).
Find the equation of the plane which passes through the point (3, 4, −1) and is parallel to the plane 2x − 3y + 5z + 7 = 0. Also, find the distance between the two planes.
Find the equation of the plane mid-parallel to the planes 2x − 2y + z + 3 = 0 and 2x − 2y + z + 9 = 0.
Find the distance between the planes \[\vec{r} \cdot \left( \hat{i} + 2 \hat{j} + 3 \hat{k} \right) + 7 = 0 \text{ and } \vec{r} \cdot \left( 2 \hat{i} + 4 \hat{j} + 6 \hat{k} \right) + 7 = 0 .\]
The distance of the line \[\vec{r} = 2 \hat{i} - 2 \hat{j} + 3 \hat{k} + \lambda\left( \hat{i} - \hat{j}+ 4 \hat{k} \right)\] from the plane \[\vec{r} \cdot \left( \hat{i} + 5 \hat{j} + \hat{k} \right) = 5\] is
Find the distance of the point (1, 1 –1) from the plane 3x +4y – 12z + 20 = 0.
Solve the following:
Find the distance of the point `3hat"i" + 3hat"j" + hat"k"` from the plane `bar"r".(2hat"i" + 3hat"j" + 6hat"k")` = 21.
Solve the following :
Find the distance of the point (13, 13, – 13) from the plane 3x + 4y – 12z = 0.
The equations of planes parallel to the plane x + 2y + 2z + 8 = 0, which are at a distance of 2 units from the point (1, 1, 2) are ________.
If the foot of perpendicular drawn from the origin to the plane is (3, 2, 1), then the equation of plane is ____________.
Find the distance of the point whose position vector is `(2hat"i" + hat"j" - hat"k")` from the plane `vec"r" * (hat"i" - 2hat"j" + 4hat"k")` = 9
Find the distance of the point (– 2, 4, – 5) from the line `(x + 3)/3 = (y - 4)/5 = (z + 8)/6`
Find the coordinates of the point where the line through (3, – 4, – 5) and (2, –3, 1) crosses the plane passing through three points (2, 2, 1), (3, 0, 1) and (4, –1, 0)
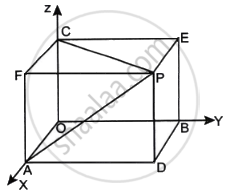
The distance of a point P(a, b, c) from x-axis is ______.
The distance of the plane `vec"r" *(2/7hat"i" + 3/4hat"j" - 6/7hat"k")` = 1 from the origin is ______.
Find the equation of the plane passing through the point (1, 1, 1) and is perpendicular to the line `("x" - 1)/3 = ("y" - 2)/0 = ("z" - 3)/4`. Also, find the distance of this plane from the origin.
S and S are the focii of the ellipse `x^2/a^2 + y^2/b^2 - 1` whose one of the ends of the minor axis is the point B If ∠SBS' = 90°, then the eccentricity of the ellipse is
A metro train starts from rest and in 5 s achieves 108 km/h. After that it moves with constant velocity and comes to rest after travelling 45 m with uniform retardation. If total distance travelled is 395 m, find total time of travelling.
The fuel charges for running a train are proportional to the square of the speed generated in miles per hour and costs ₹ 48 per hour at 16 miles per hour. The most economical speed if the fixed charges i.e. salaries etc. amount to ₹ 300 per hour is
`phi` is the angle of the incline when a block of mass m just starts slipping down. The distance covered by the block if thrown up the incline with an initial speed u0 is
The coordinates of the point on the parabola y2 = 8x which is at minimum distance from the circle x2 + (y + 6)2 = 1 are
The equations of motion of a rocket are:
x = 2t,y = –4t, z = 4t, where the time t is given in seconds, and the coordinates of a ‘moving point in km. What is the path of the rocket? At what distances will the rocket be from the starting point O(0, 0, 0) and from the following line in 10 seconds? `vecr = 20hati - 10hatj + 40hatk + μ(10hati - 20hatj + 10hatk)`
Find the distance of the point (2, 3, 4) measured along the line `(x - 4)/3 = (y + 5)/6 = (z + 1)/2` from the plane 3x + 2y + 2z + 5 = 0.
Find the distance of the point (1, –2, 0) from the point of the line `vecr = 4hati + 2hatj + 7hatk + λ(3hati + 4hatj + 2hatk)` and the point `vecr.(hati - hatj + hatk)` = 10.
The acute angle between the line `vecr = (hati + 2hatj + hatk) + λ(hati + hatj + hatk)` and the plane `vecr xx (2hati - hatj + hatk)` is ______.
Find the coordinates of points on line `x/1 = (y - 1)/2 = (z + 1)/2` which are at a distance of `sqrt(11)` units from origin.
If the points (1, 1, λ) and (–3, 0, 1) are equidistant from the plane `barr*(3hati + 4hatj - 12hatk) + 13` = 0, find the value of λ.
The distance of the point `2hati + hatj - hatk` from the plane `vecr.(hati - 2hatj + 4hatk)` = 9 will be ______.
Find the equations of the planes parallel to the plane x – 2y + 2z – 4 = 0 which is a unit distance from the point (1, 2, 3).
In the figure given below, if the coordinates of the point P are (a, b, c), then what are the perpendicular distances of P from XY, YZ and ZX planes respectively?