Advertisements
Advertisements
प्रश्न
दो कण जिनमें से प्रत्येक का द्रव्यमान m एवं चाल ν है, d दूरी पर समान्तर रेखाओं के अनुदिश, विपरीत दिशाओं में चल रहे हैं। दर्शाइए कि इस द्विकण निकाय का सदिश कोणीय संवेग समान रहता है, चाहे हम जिस बिन्दु के परितः कोणीय संवेग लें।
उत्तर
मान लिया जाता है कि एक निश्चित क्षण में दो कण क्रमश: बिंदु P और Q पर स्थित हैं।
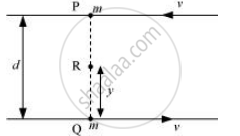
बिंदु P के परितः इस प्रणाली का कोणीय संवेग:
`vecL_p = mv xx 0 + mv xx d`
= mvd ....(i)
बिंदु Q के परितः इस प्रणाली का कोणीय संवेग:
`vecL_Q = mv xx d + mv xx 0`
= mvd ....(ii)
बिंदु R को माना जाता है, जो कि बिंदु Q से y दूरी पर है, अर्थात,
QR = y
∴ PR = d – y
बिंदु R के परितः इस प्रणाली का कोणीय संवेग:
`vecL_R = mvxx(d-y) + mv xx y`
= mvd - mvy + mvy
=mvd ...(iii)
समीकरण i, ii और iii से,
`vecL_p = vecL_Q = vecL_R` .... (iv)
समीकरण (iv) से हम यह निष्कर्ष निकालते हैं कि कोणीय संवेग उस बिन्दु पर निर्भर नहीं करता जिसके परितः यह लिया जाता है।
