Advertisements
Advertisements
प्रश्न
W भार की एक असंमांग छड़ को, उपेक्षणीय भार वाली दो डोरियों से चित्र में दर्शाए अनुसार लटका कर विरामावस्था में रखा गया है। डोरियों द्वारा ऊध्र्वाधर से बने कोण क्रमशः 36.9° एवं 53.1° हैं। छड़ 2 m लम्बाई की है। छड़ के बाएँ सिरे से इसके गुरुत्व केन्द्र की दूरी d ज्ञात कीजिए।
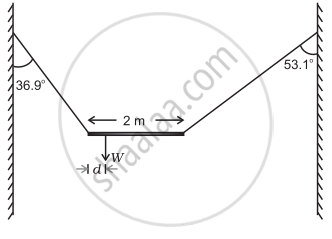
उत्तर
माना छड़ AB का गुरुत्व केन्द्र G, उसके एक सिरे A से ‘d दूरी पर स्थित है। छड़ तीन बलों के अधीन सन्तुलन में है।
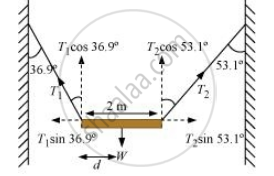
डोरियों में तनाव T1 तथा T2 डोरियों के अनुदिश ऊपर 3 की ओर कार्य करते हैं।
छड़ का भार W उसके गुरुत्व केन्द्र G पर ऊर्ध्वाधरत: नीचे की ओर कार्य करता है।
सन्तुलन की स्थिति में तीनों बलों की क्रिया-रेखाएँ एक ही बिन्दु O पर काटती हैं।
∠AOG = 36.9°,
∠BOG = 53.1°
GC ⊥ AO, GD ⊥ BO∠GAC = 90°-∠GOA = 90° - 36.9° = 53.1°
∠GBD = 90° - ∠GOB = 90° - 53.1° = 36.9°
बलों के क्षैतिज घटको का योग
`"T"_1 "sin" 36.9^circ - "T"_2 "sin" 53.1^circ = 0`
⇒ `"T"_1 "sin" 36.9^circ = "T"_2 "sin" 53.1^circ` ...(1)
बिन्दु G के परितः आघूर्ण लेने पर,
`"T"_2"GD" - "T"_1"GC" = 0` ...[∵ W का G के परितः आघूर्ण = 0]
या T2 GB sin ∠GBD = T1GA sin ∠GAC
या `"T"_2 (2 - "d") "sin" 36.9^circ = "T"_1 "d" "sin" 53.1^circ` [∵ AB = 2 m]
या `"T"_1 "d" "sin" 53.1^circ = "T"_2 (2 - "d") "sin" 36.9^circ` ...(2)
समीकरण (2) को समीकरण (1) से भाग देने पर,
`"d"("sin" 53.1^circ)/("sin" 36.9^circ) = ((2 - "d") "sin" 36.9^circ)/("sin" 53.1^circ)`
= `"d" ("sin" 53.1^circ)/("cos" 53.1^circ) = (2 - "d")("cos" 53.1^circ)/("sin" 53.1^circ)` ...[∵ sin 36.9° = sin (90° - 53.1°)]
या `"d" "tan"^2 53.1° = (2 - "d")`
या d(177) = 2 - d ...[∵ tan 53.1° = 1.33]
या 2.77 d = 2
`"d" = 2/2.77`
= 0.72 m
अतः छड़ का गुरुत्व केंद्र सिरे A से 0.72 m दूर दूसरे सिरे की ओर है।
