Advertisements
Advertisements
प्रश्न
दो समरूप त्रिभुजों के क्षेत्रफल 225 वर्ग सेमी तथा 81 वर्ग सेमी है। यदि छोटे त्रिभुज की एक भुजा की लंबाई 12 सेमी हो तो बड़े त्रिभुज की संगत भुजा की लंबाई ज्ञात कीजिए।
उत्तर
माना, वे दो समरूप त्रिभुज, ΔABC तथा ΔPQR है |
ΔABC यह ΔPQR से बड़ा त्रिभुज है |
∴ A(ΔABC) = 225 वर्गसेमी तथा A(ΔPQR) = 81 वर्गसेमी और PQ = 12 सेमी
∴ `("A"(Δ"ABC"))/("A"(Δ"PQR")) = "AB"^2/"PQ"^2` .........(समरूप त्रिभुजों के क्षेत्रफल का प्रमेय)
∴ `225/81 = "AB"^2/(12)^2` .......(दिया गया मान रखने पर)
∴ `15/9 = "AB"/12` .........(दोनों पक्षों का वर्गमूल लेने पर)
∴ AB = `(15 xx 12)/9` = 20 सेमी
∴ बड़े त्रिभुज की संगत भुजा की लंबाई 20 सेमी है |
APPEARS IN
संबंधित प्रश्न
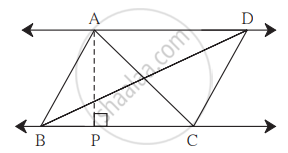
संलग्न आकृति में AP ⊥ BC, AD || BC, तो A(ΔABC) : A(ΔBCD) का मान ज्ञात कीजिए।
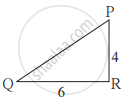
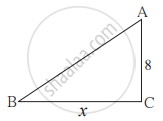
आकृति में दर्शाएअनुसार 8 मीटर तथा 4 मीटर ऊँचाईवाले दो खंभे समतल जमीन पर खड़े हैं। सूर्य के प्रकाश से छोटे खंभे की परछाई 6 मीटर होती हो तो उसी समय बड़े खंभे की परछाईं की लंबाई कितनी होगी?
ΔABC ~ ΔPQR, A(ΔABC) = 80, A(ΔPQR) = 125 तो निम्नलिखित रिक्त चौखटों को पूरा कीजिए।
`("A"(Δ"ABC"))/("A"(Δsquare)) = 80/125 = square/square`
∴ `"AB"/"PQ" = square/square`
ΔLMN ~ ΔPQR, 9 × A(ΔPQR ) = 16 × A (ΔLMN), यदि QR = 20 तो MN का मान ज्ञात कीजिए।
समबाहु ΔABC तथा ΔDEF में, A(ΔABC) : A(ΔDEF) = 1 : 2 होने पर AB = 4 हो तो DE की लंबाई कितनी?
ΔABC में B – D – C और BD = 7, BC = 20, तो निम्नलिखित अनुपात ज्ञात कीजिए।
`(A(∆ABD))/(A(∆ABC))`
ΔABC में B - D – C और BD = 7, BC = 20 तो निम्नलिखित अनुपात ज्ञात कीजिए।
`("A"(Δ"ADC"))/("A"(Δ"ABC"))`
ΔMNT ~ ΔQRS, बिंदु T से खींचे गए शीर्षलंब की लंबाई 5 तथा बिंदु S से खींचे गए शीर्षलंब की लंबाई 9 है, तो `("A"(Δ"MNT"))/("A"(Δ"QRS"))` यह अनुपात ज्ञात कीजिए।
यदि ΔABC ∼ΔPQR, AB : PQ = 4 : 5 तथा A(ΔPQR) = 125 सेमी2 हो, तो A(ΔABC) का मान ज्ञात करो.
यदि Δ ABC और ~ Δ PQR और AB : PQ = 2 : 3 तो `(A(Δ "ABC"))/(A(Δ "PQR")` का मान ज्ञात कीजिए।
