Advertisements
Advertisements
प्रश्न
समबाहु ΔABC तथा ΔDEF में A(ΔABC) : A(ΔDEF) = 1 : 2 AB = 4 तो DE की लंबाई ज्ञात कीजिए।
उत्तर
ΔABC और ΔDEF समबाहु त्रिभुज है |
∴ ∠A = ∠B = ∠C = ∠D = ∠E = ∠F = 60° ..........(समबाहु त्रिभुज के कोण)
ΔABC और ΔDEF में,
`{:(∠"A" ≅ ∠"D"), (∠"B" ≅ ∠"E"):}}` .........(प्रत्येक 60°)
∴ ΔABC ∼ ΔDEF ........(समरूपता की को-को कसौटी)
समरूप त्रिभुजों के क्षेत्रफल के प्रमेय से,
`("A"(Δ"ABC"))/("A"(Δ"DEF")) = "AB"^2/"DE"^2` ....(1)
A(ΔABC) : A(ΔDEF) = 1 : 2 तथा AB = 4 ......(दिया है |) .....(2)
∴ `1/2 = 4^2/"DE"^2` .....[(1) और (2) से]
∴ `"DE"^2 = 4^2 xx 2`
∴ DE = `4sqrt2` ........(दोनों पक्षों का वर्गमूल लेने पर)
∴ DE = `underline(4sqrt2)`.
APPEARS IN
संबंधित प्रश्न
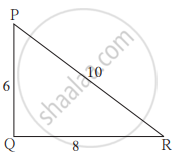
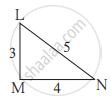
संलग्न आकृति में, दिए गए त्रिभुज क्या समरूप हैं? यदि हाँ तो किस कसौटी के अनुसार?
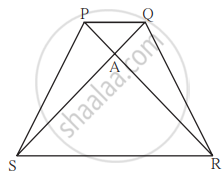
संलग्न आकृति में `square`PQRS एक समलंब चतुर्भुज है। जिसमें भुजा PQ || भुजा SR, AR = 5AP, AS = 5AQ तो सिद्ध कीजिए कि, SR = 5PQ
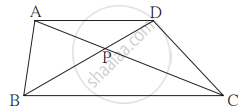
समलंब चतुर्भुज ABCD में, भुजा AB || भुजा DC विकर्ण AC तथा विकर्ण BD परस्पर बिंदु O पर प्रतिच्छेदित करते हैं। यदि AB = 20, DC = 6, OB = 15 तो OD का मान ज्ञात कीजिए।
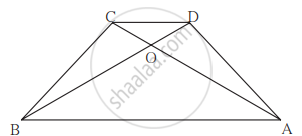
`square`ABCD एक समांतर चतुर्भुज है। भुजा BC पर E कोई एक बिंदु है ; रेखा DE रेख AB को बिंदु T पर प्रतिच्छेदित करती है । तो सिद्ध कीजिए कि DE × BE = CE × TE।
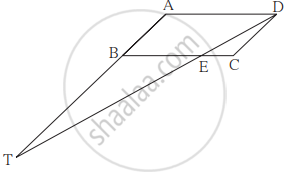
संलग्न आकृति में रेख AC तथा रेख BD परस्पर बिंदु P पर प्रतिच्छेदित करते हैं और `"AP"/"CP" = "BP"/"DP"` तो सिद्ध कीजिए कि, ΔABP ∼ ΔCDP.
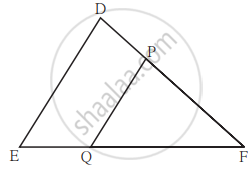
आकृति में रेख PQ || रेख DE यदि A(ΔPQF) = 20 वर्ग इकाई, PF = 2 DP है, तो A(`square`DPQE) ज्ञात करने के लिए निम्नलिखित कृति पूर्ण कीजिए।
A(ΔPQF) = 20 वर्ग इकाई, PF = 2 DP, माना DP = x ∴ PF = 2x
DF = DP + `square = square + square = 3x`
ΔFDE तथा ΔFPQ में।
∠FDE ≅ ∠`square` (संगत कोण)
∠FED ≅ ∠`square` (संगत कोण)
∴ ΔFDE ∼ ΔFPQ .........(को-को कसौटी)
∴ `("A"(Δ"FDE"))/("A"(Δ"FPQ")) = square/square = (3x)^2/(2x)^2 = 9/4`
A(ΔFDE) = `9/4`A(ΔFPQ ) = `9/4 xx square = square`
A(`square`DPQE) = A(ΔFDE) - A(ΔFPQ)
= `square - square`
= `square`
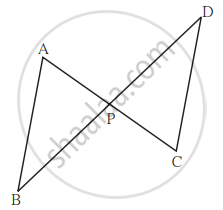
`square`ABCD में रेख AD || रेख BC. विकर्ण AC और विकर्ण BD परस्पर एक दूसरे को बिंदु P पर प्रतिच्छेदित करते हैं। तो सिद्ध कीजिए कि `"AP"/"PD" = "PC"/"BP"`
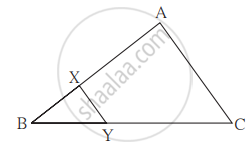
आकृति में रेख XY || भुजा AC. यदि 2AX = 3BX और XY = 9 तो AC का मान ज्ञात करने के लिए निम्नलिखित कृति पूर्ण कीजिए।
कृति : 2AX = 3BX
∴ `"AX"/"BX" = square/square`
`("AX + BX")/"BX" = (square + square)/square` ........... (योगानुपात की क्रिया से)
`"AB"/"BX" = square/square` .......... (I)
ΔBCA ~ ΔBYX .......... (समरूपता की `square` कसौटी)
∴ `"BA"/"BX" = "AC"/"XY"` .......... (समरूप त्रिभुजों की संगत भुजा)
∴ `square/square = "AC"/9`
∴ AC = `square` ..........(I) से
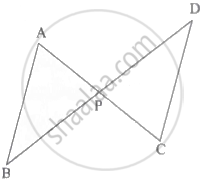
दी गई आकृति में, रेख AC तथा रेख BD एक-दूसरे को बिंदु P पर प्रतिच्छेदित करते हैं।
यदि `(AP)/(CP) = (BP)/(DP)` हो, तो ΔABP ∼ ΔCDP सिद्ध करने के लिए निम्न कृति पूर्ण करो:
कृति: ΔABP तथा ΔCDP में,
`(AP)/(CP) = (BP)/(DP)` ..........`square`
∠APB ≅ `square` ...(शीर्षाभिमुख कोण)
∴ `square` ∼ ΔCDP ... (समरूपता की `square` कसोटी)
ΔABC में, रेख XY || रेख AC. यदि 2AX = 3BX तथा XY = 9 हो, तो AC का मान ज्ञात करो।