Advertisements
Advertisements
प्रश्न
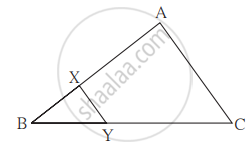
आकृति में रेख XY || भुजा AC. यदि 2AX = 3BX और XY = 9 तो AC का मान ज्ञात करने के लिए निम्नलिखित कृति पूर्ण कीजिए।
कृति : 2AX = 3BX
∴ `"AX"/"BX" = square/square`
`("AX + BX")/"BX" = (square + square)/square` ........... (योगानुपात की क्रिया से)
`"AB"/"BX" = square/square` .......... (I)
ΔBCA ~ ΔBYX .......... (समरूपता की `square` कसौटी)
∴ `"BA"/"BX" = "AC"/"XY"` .......... (समरूप त्रिभुजों की संगत भुजा)
∴ `square/square = "AC"/9`
∴ AC = `square` ..........(I) से
उत्तर
2AX = 3BX
∴ `"AX"/"BX" = underline(3/2)`
`("AX + BX")/"BX" = underline((3 + 2)/2)` ........... (योगानुपात की क्रिया से)
`"AB"/"BX" = underline(5/2)` .......... (I)
ΔBCA ~ ΔBYX .......... (समरूपता की को-को कसौटी)
∴ `"BA"/"BX" = "AC"/"XY"` .......... (समरूप त्रिभुजों की संगत भुजा)
∴ `underline(5/2) = "AC"/9`
∴ AC = 22.5 ..........(I) से
APPEARS IN
संबंधित प्रश्न
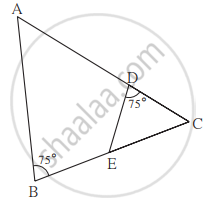
आकृति में ∠ABC = 75°, ∠EDC = 75° तो इनमें दो त्रिभुज किस कसौटी के अनुसार समरूप हैं? उनकी समरूपता की एकैकी संगति लिखिए।
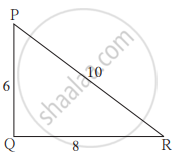
संलग्न आकृति में, दिए गए त्रिभुज क्या समरूप हैं? यदि हाँ तो किस कसौटी के अनुसार?
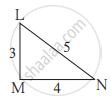
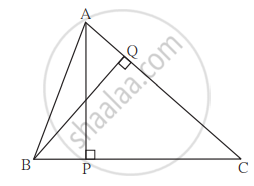
ΔABC में AP ⊥ BC, BQ ⊥ AC B-P-C, A-Q-C तो सिद्ध कीजिए कि ΔCPA ~ ΔCQB। यदि AP = 7, BQ = 8, BC = 12 तो AC का मान ज्ञात कीजिए।
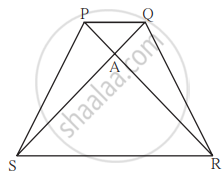
संलग्न आकृति में `square`PQRS एक समलंब चतुर्भुज है। जिसमें भुजा PQ || भुजा SR, AR = 5AP, AS = 5AQ तो सिद्ध कीजिए कि, SR = 5PQ
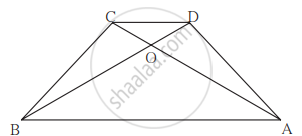
समलंब चतुर्भुज ABCD में, भुजा AB || भुजा DC विकर्ण AC तथा विकर्ण BD परस्पर बिंदु O पर प्रतिच्छेदित करते हैं। यदि AB = 20, DC = 6, OB = 15 तो OD का मान ज्ञात कीजिए।
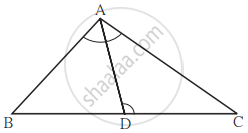
संलग्न आकृति में ΔABC में बिंदु D यह भुजा BC पर इस प्रकार है, कि ∠BAC = ∠ADC तो सिद्ध कीजिए कि, CA2 = CB × CD.
समबाहु ΔABC तथा ΔDEF में A(ΔABC) : A(ΔDEF) = 1 : 2 AB = 4 तो DE की लंबाई ज्ञात कीजिए।
दी गई आकृति में, रेख AC तथा रेख BD एक-दूसरे को बिंदु P पर प्रतिच्छेदित करते हैं।
यदि `(AP)/(CP) = (BP)/(DP)` हो, तो ΔABP ∼ ΔCDP सिद्ध करने के लिए निम्न कृति पूर्ण करो:
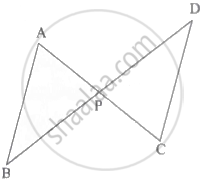
कृति: ΔABP तथा ΔCDP में,
`(AP)/(CP) = (BP)/(DP)` ..........`square`
∠APB ≅ `square` ...(शीर्षाभिमुख कोण)
∴ `square` ∼ ΔCDP ... (समरूपता की `square` कसोटी)
□ABCD समांतर चतुर्भुज है। बिंदु P, भुजा CD का मध्यबिंदु है। रेख BP यह विकर्ण AC को बिंदु X पर प्रतिच्छेदित करती है, तो सिद्ध करो कि 3AX = 2AC.
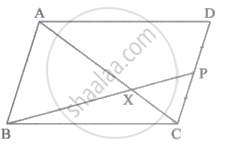
`square`ABCD एक समलंब चतुर्भुज है। AB || CD समलंब `square`ABCD के विकर्ण परस्पर बिंदु P में प्रतिच्छेदित करते हैं।
इस आधार पर नीचे दिए प्रश्नों के उत्तर लिखिए:
- दी गई जानकारी के आधार पर आकृति बनाइये।
- उस आधार पर एकांतर कोणों की तथा शीर्षाभिमुख कोणों की जोड़ियाँ लिखिए।
- समरूपता की कसौटीसह समरूप त्रिभुओं के नाम लिखिए।
