Advertisements
Advertisements
प्रश्न
`square`ABCD एक समलंब चतुर्भुज है। AB || CD समलंब `square`ABCD के विकर्ण परस्पर बिंदु P में प्रतिच्छेदित करते हैं।
इस आधार पर नीचे दिए प्रश्नों के उत्तर लिखिए:
- दी गई जानकारी के आधार पर आकृति बनाइये।
- उस आधार पर एकांतर कोणों की तथा शीर्षाभिमुख कोणों की जोड़ियाँ लिखिए।
- समरूपता की कसौटीसह समरूप त्रिभुओं के नाम लिखिए।
उत्तर

- एकांतर कोण: ∠BAP = ∠PCD
शीर्षाभिमुख कोण: ∠APB = ∠CPD - ΔAPB ∼ ΔCPD .......(कोको कसौटी)
APPEARS IN
संबंधित प्रश्न
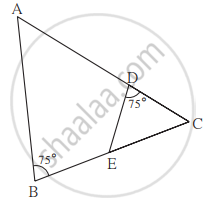
आकृति में ∠ABC = 75°, ∠EDC = 75° तो इनमें दो त्रिभुज किस कसौटी के अनुसार समरूप हैं? उनकी समरूपता की एकैकी संगति लिखिए।
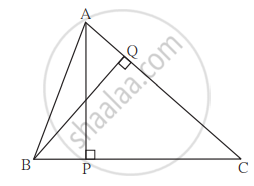
ΔABC में AP ⊥ BC, BQ ⊥ AC B-P-C, A-Q-C तो सिद्ध कीजिए कि ΔCPA ~ ΔCQB। यदि AP = 7, BQ = 8, BC = 12 तो AC का मान ज्ञात कीजिए।
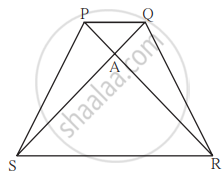
संलग्न आकृति में `square`PQRS एक समलंब चतुर्भुज है। जिसमें भुजा PQ || भुजा SR, AR = 5AP, AS = 5AQ तो सिद्ध कीजिए कि, SR = 5PQ
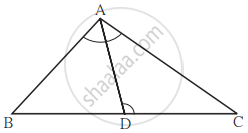
संलग्न आकृति में ΔABC में बिंदु D यह भुजा BC पर इस प्रकार है, कि ∠BAC = ∠ADC तो सिद्ध कीजिए कि, CA2 = CB × CD.
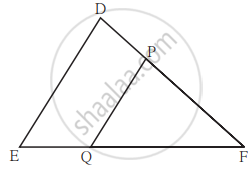
आकृति में रेख PQ || रेख DE यदि A(ΔPQF) = 20 वर्ग इकाई, PF = 2 DP है, तो A(`square`DPQE) ज्ञात करने के लिए निम्नलिखित कृति पूर्ण कीजिए।
A(ΔPQF) = 20 वर्ग इकाई, PF = 2 DP, माना DP = x ∴ PF = 2x
DF = DP + `square = square + square = 3x`
ΔFDE तथा ΔFPQ में।
∠FDE ≅ ∠`square` (संगत कोण)
∠FED ≅ ∠`square` (संगत कोण)
∴ ΔFDE ∼ ΔFPQ .........(को-को कसौटी)
∴ `("A"(Δ"FDE"))/("A"(Δ"FPQ")) = square/square = (3x)^2/(2x)^2 = 9/4`
A(ΔFDE) = `9/4`A(ΔFPQ ) = `9/4 xx square = square`
A(`square`DPQE) = A(ΔFDE) - A(ΔFPQ)
= `square - square`
= `square`
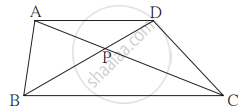
`square`ABCD में रेख AD || रेख BC. विकर्ण AC और विकर्ण BD परस्पर एक दूसरे को बिंदु P पर प्रतिच्छेदित करते हैं। तो सिद्ध कीजिए कि `"AP"/"PD" = "PC"/"BP"`
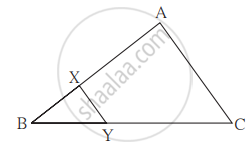
आकृति में रेख XY || भुजा AC. यदि 2AX = 3BX और XY = 9 तो AC का मान ज्ञात करने के लिए निम्नलिखित कृति पूर्ण कीजिए।
कृति : 2AX = 3BX
∴ `"AX"/"BX" = square/square`
`("AX + BX")/"BX" = (square + square)/square` ........... (योगानुपात की क्रिया से)
`"AB"/"BX" = square/square` .......... (I)
ΔBCA ~ ΔBYX .......... (समरूपता की `square` कसौटी)
∴ `"BA"/"BX" = "AC"/"XY"` .......... (समरूप त्रिभुजों की संगत भुजा)
∴ `square/square = "AC"/9`
∴ AC = `square` ..........(I) से
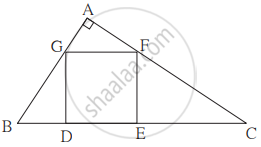
आकृति में `square`DEFG एक वर्ग है। ΔABC में ∠A = 90°, बिंदु F भुजा AC पर स्थित है। तो सिद्ध कीजिए कि, DE2 = BD × EC (ΔGBD तथा ΔCFE को समरूप दिखाइए और GD = FE = DE का उपयोग कीजिए।)
दी गई आकृति में, रेख AC तथा रेख BD एक-दूसरे को बिंदु P पर प्रतिच्छेदित करते हैं।
यदि `(AP)/(CP) = (BP)/(DP)` हो, तो ΔABP ∼ ΔCDP सिद्ध करने के लिए निम्न कृति पूर्ण करो:
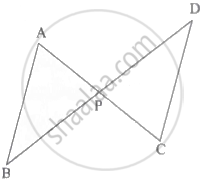
कृति: ΔABP तथा ΔCDP में,
`(AP)/(CP) = (BP)/(DP)` ..........`square`
∠APB ≅ `square` ...(शीर्षाभिमुख कोण)
∴ `square` ∼ ΔCDP ... (समरूपता की `square` कसोटी)
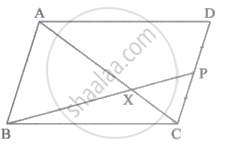
□ABCD समांतर चतुर्भुज है। बिंदु P, भुजा CD का मध्यबिंदु है। रेख BP यह विकर्ण AC को बिंदु X पर प्रतिच्छेदित करती है, तो सिद्ध करो कि 3AX = 2AC.